Notes for Mechanics class for Spring 2023.
- Chapter 1
- Chapter 2
- Chapter 3
- Chapter 4
- Chapter 5
- Chapter 6
- Chapter 7
- Chapter 8
- Chapter 9
- Chapter 10
- Chapter 11
Chapter 1
Main Concepts
Scalars, Vectors and Matrices
- A scalar is some quantity that is invariant under any coordinate transformation
- A vector is an object in $\mathbb{R^{n}}$ that is invariant under rotations
- Vectors are closed under addition and scalar multiplication
- The Dot product is defined as $\vec{A}\cdot \vec{B} = \Sigma_{i} A_{i}B_{i}$ or equivalently $\vec{A}\cdot \vec{B} = |A| |B| \cos(\vec{A},\vec{B})$
- $|A| = \sqrt{\Sigma_{i} A_{i}^{2}}$
- This is invariant under rotation (since it is a scalar)
- Abelian
- The Cross Product is defined as $C = A \times B$ where $C_{i} = \Sigma_{j,k} \epsilon_{ijk}A_{j}B_{k}$ whre $\epsilon_{ijk}$ is the Levi-Civata tensor (0 if indices are the same, 1 if an even permutation of 1,2,3 and -1 if an odd permutation of 1,2,3)
- Alternatively $|C| = |A||B|\sin\theta$
- Non-Abelian
- $A\times(B\times C) = (A\cdot C)B-(A\cdot B)C$
- $A\cdot (B\times C) = B\cdot (C\times A) = C \cdot (A\times B) = ABC$
- Matrices are objects in $\mathbb{R^{n\times m}}$
- A simple 2D rotation is given by (can be derived by rotating the primed coordinate system around the orign by some angle and adding up lengths)
- $x_1^{’} = x_1 \cos \theta +x_2 \sin \theta$
- $x_2^{’} = -x_1 \sin \theta +x_2 \cos \theta$
- In general $x_{i} = \Sigma_{j=1}^{3} \lambda_{ji} x_{j}^{’}$ where the $\lambda$ are the directional cosines defined by $\lambda_{ij} = \cos(x_{i}^{’},x_j)$ ie. the cosine of the angle b/w the axes
- The inverse transform is such that $\Sigma_{i}\lambda_{ij}\lambda_{ik} =\delta_{jk}$
- For orthogonal (ie. rotation matrices), we have that $\lambda^{T} = \lambda^{-1}$ and that det($\lambda = \pm 1$), where the -1 refers to a changing of handedness
- A simple 2D rotation is given by (can be derived by rotating the primed coordinate system around the orign by some angle and adding up lengths)
Derivatives of Position
- In standard Cartesian coordinates, we have that position is given by $\vec{r} = a \hat{x}+b \hat{y}+c \hat{z}$
- In any non-Cartesian coordinates, the basis vectors themselves change as a function of time.
- For polar coordinates, we have that
- $\dot{\hat{r}} = \dot{\theta}\hat{\theta}$
- $\dot{\hat{\theta}} = -\dot{\theta}\hat{r}$
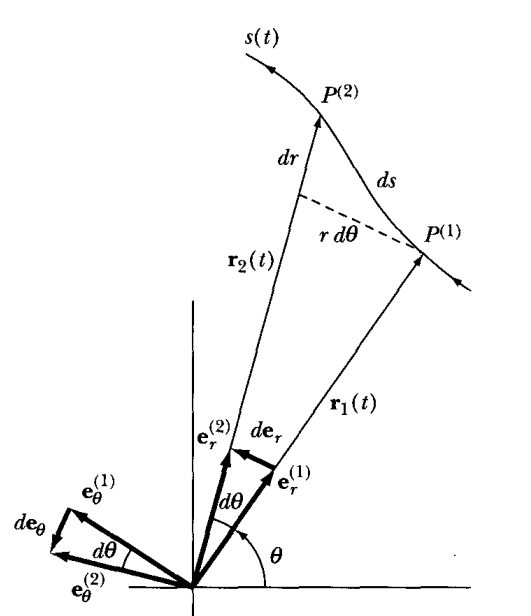
- Hence, the velocity and acceleration in polar coordinates are
- $\vec{v} = \dot{r}\hat{r}+r\dot{\theta}\hat{\theta}$
- $\vec{a} = (\ddot{r}-r\theta^2)\hat{r}+(r\ddot{\theta}^{2}+\dot{r}\dot{\theta})\hat{\theta}$
- We can define $\omega = \dot{\theta}$ and define $\vec{v} = \omega \times \vec{r}$
- For polar coordinates, we have that
Chapter 2
Main Concepts
Newton’s Laws
- A body remains at rest or in uniform motion unless acted upon by a force
- A body acted upon by a force moves in such a manner that the time rate of change of momentum equals the force
- If two bodies exert forces on each other, these forces are equal in magnitude and opposite in direction
- These laws are only valid in inertial frames of reference (ie. frames where objects move in straight lines when subject to no external force). If you are in a non-inertial frame, you need to introduce forces that explain this deviation from straight lines
- Much of Mechanics comes down to solving the equation $\vec{m\ddot{r}} = \vec{F(\vec{r},\vec{v},t)}$
Definitions
- Momentum p is given by $\vec{p} = m\vec{v}$
- Force F is given by $\frac{d\vec{p}}{dt} = \frac{d}{dt}(m\vec{v})$
- inertial mass (the mass of F=ma) and gravitational mass (the mass in the law of gravitation) are the same
Conservation Laws
- Momentum is conserved when the net force on a system is zero (ie $\dot{p} = 0$)
- Define angular momentum as $\vec{L} = \vec{r}\times \vec{p} = I\omega$ and torque as $\vec{T} = \vec{r}\times \vec{F} = I\alpha$
- $\frac{d\vec{L}}{dt} = \vec{T}$
- Hence, when the net torque is 0, angular momentum is conserved
- Define Work as $\int \vec{F}\cdot \vec{dr}$, kinetic energy as $\frac{mv^2}{2}$. Define the potential U as $\vec{F} = -\nabla U$
- The work is given by the change in kinetic energy
- The total energy E is T+U is conserved as long as the force is not time-dependent
- From the potential energy, we can determine the stability of a solution at equilibrium (ie when $\frac{dU}{dx} = 0$)
- if $\frac{d^{2}U}{d^{2}x} >0$ we are stable, if $\frac{d^{2}U}{d^{2}x} <0$, we are unstable
Chapter 3
Main Concepts
- $\vec{F} = -kx$ where $K = -\frac{dF}{dx}$ is called Hooke’s Law
- For an SHO, we have that $\ddot{x}+\omega_0^2x = 0$ where $\omega_0 = \sqrt{\frac{k}{m}}$
- $\omega_0 =2\pi \nu_0$
- $\nu_0 = \frac{1}{\tau_0}$
- For a damped oscillator with a linear friction term of the form $-b\dot{x}$, we have that
- $\ddot{x}+2\beta\dot{x}+\omega_{0}^{2}x = 0$ where $\beta = \frac{b}{2m}$
- The general solution has the form of $x(t) = e^{-\beta t}(A_{1}exp(t\sqrt{\beta^{2}-\omega_{0}^{2}})+A_{2}exp(-t\sqrt{\beta^{2}-\omega_{0}^{2}}))$
- $\omega_{0}^{2} > \beta^{2}$ is underdamping
- function oscillates, but dies off over time
- $\omega_{0}^{2} = \beta^{2}$ is critial damping
- you much change the form of x(t) to becomes $x(t) = (A+Bt)e^{-\beta t} $
- This system returns to zero faster than any other system
- $\omega_{0}^{2} < \beta^{2}$ is over damping
- Sytem returns to zero slower than critically damped
- $\omega_{0}^{2} > \beta^{2}$ is underdamping
- For a forced damped oscillator with a linear friction term, we have that $\ddot{x}+2\beta\dot{x}+\omega_{0}^{2}x = A \cos (\omega t)$
- The particular solution takes the form of $D \cos(\omega t-\delta)$ where you need to solve for what D and $\delta$ are by comparing the coefficient of the sin and cosine terms after differentiating
- You also need the complementary solution from solving the regular damped oscillator
- When $\omega = \omega_{R}$ where $\omega_{R} = \sqrt{\omega_{0}^{2}-2\beta^2}$, you get resonance, which is the frequency that produces the maximum amplitude response
- The quality factor Q is defined to be $\frac{\omega_{R}}{2\beta}$. Q is large when little damping occurs
- For any periodic driving term ($F(t_\tau) = F(t)$), we can see that $F(t) =\frac{a_0}{2}+\Sigma_{n=1}^{\infty}(a_{n}\cos (n\omega t)+b_{n}\sin (n\omega t))$ where
- $a_{n} = \frac{2}{\tau}\int_{0}^{\tau} F(t’)\cos (n\omega t’) dt'$
- $b_{n} = \frac{2}{\tau}\int_{0}^{\tau} F(t’)\sin (n\omega t’) dt'$
Chapter 4
Main Concepts
- A differential equation is non-linear if it contains powers of $\dot{x}$ and x higher than linear, or if it contains cross terms xy, or if it contains non-linear functions of x
- Deterministic chaos refers to the motion of a system whose time evolution is sensitivty to the initial conditions
Nonlinear Oscillations
- When the deviation from linearity of an oscillator is symmetric (ie. the force at -x equals the force at x), then the new force becomes $F(x) = -kx+\epsilon x^3$, which has a corresponding potential of $U(x) = \frac{kx^2}{2}-\frac{\epsilon x^2}{4}$
- $\epsilon > 0$ is called soft since the new force is less than the linear term alone
- $\epsilon <0$ is called hard
- For the antisymmetric case, we have that $F(x) = -kx+\lambda x^3$ with $U(x) = \frac{kx^2}{2}-\frac{\lambda x^3}{3}$
Phase diagrams
- From energy considerations, we know that $\dot{x} \propto \sqrt{E-U(x)}$. Hence, if U(x) is known, we can construct the phase diagram easily
- For systems with damping, computers can construct phase paths quite easily from a given set of initial conditions
- Stable orbits look like ellipses or inwards spirals
- Unstable orbits spiral outward
Plane Pendulum
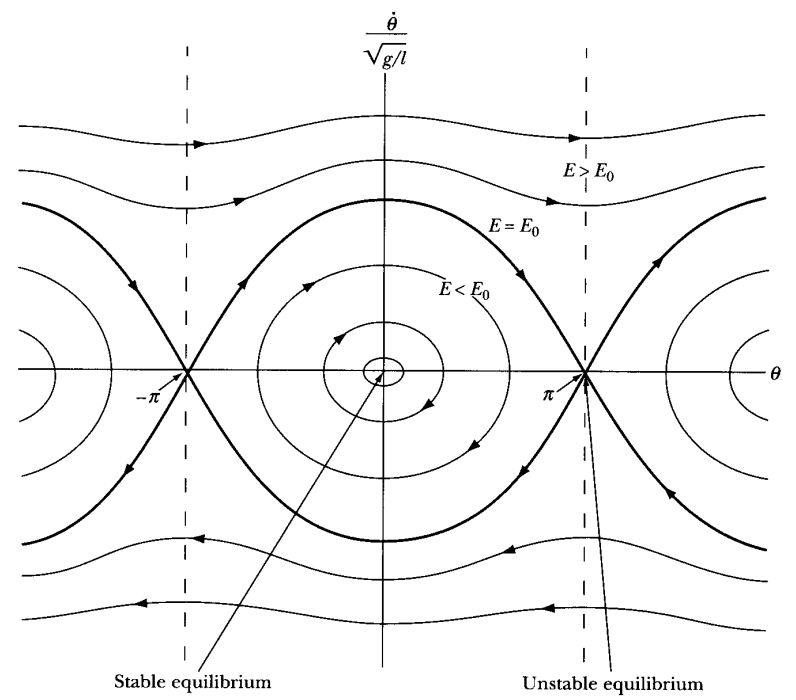
- Closed orbits are stable orbits
- The unit cell refers to the region between $-\pi$ and $\pi$, since this region is repeated
- The period of the system is energy dependent
- FOr energies larger than $E_{0}$, the motion corresponds to the pendulum executing complete revolutions around its support axis
Chapter 5
Main Concepts
- $\vec{F} = \frac{-GmM}{r^2}\hat{r}$
- $\vec{F} = -Gm \int \frac{\rho(r’)}{r^2} e_{r} dv'$
- $r’$ location of mass density w.r.t. origin and r distance b/w mass density and test mass
- Potential $V = -G \int \frac{pho}{r} dv'$
- Potential energy is $U = mV$ an the force is $F -\nabla U$
- $V = \frac{-GM}{r}$ for a point mass and when outside a sphere with spherically symmetric mass distribution
- $\nabla^2 V = 4 \pi G \rho$
Chapter 6
Main Concepts
- $\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y} = 0$
- f is a function of the form $f(x,y,y’)$ whose extrema you are trying to find
- Alternatively, we can say that $\frac{\partial f}{\partial x}-\frac{d}{dx}(f-y’\frac{\partial f}{\partial y’}) =0$. This is useful when f is not explicitly dependent on x, which implies that $f-y\frac{\partial f}{\partial y’} = const$
- With the addition of constraints of the form $g(y,x) = 0$, we have that $\frac{\partial f}{\partial y}-\frac{d}{dx}\frac{\partial f}{\partial y’}+\Sigma_{j} \lambda_{j}(x)\frac{\partial g_{j}}{\partial y_{j}}= 0$
Chapter 7
Main Concepts
- Define your lagrangian as $\mathcal{L} = T-U$. The Euler Lagrange equations then become $\frac{\partial L}{\partial x}-\frac{d}{dx}\frac{\partial L}{\partial \dot{x}} = 0$
- These can be modified to include constraints of the form $g(q)=0$: $\mathcal{L} = \frac{\partial L}{\partial q}-\frac{d}{dt}\frac{\partial L}{\partial \dot{q}}+\Sigma_{j}\lambda_{j}(t)\frac{\partial g_{j}}{\partial q} = 0$
- The force of constraint them becomes $F_{j} = \Sigma_{k} \lambda_{k} \frac{\partial f_{k}}{\partial q_{j}}$
- You have a conserved quantity from Noether’s theorem whenever $\frac{\partial \mathcal{L}}{\partial q} = 0$
- The Hamiltonian is defined as $(\Sigma_{j} p_{j}\dot{q}{j}) -L$ where $p{j} = \frac{\partial \mathcal{L}}{\partial \dot{q_{j}}}$
- The equations of motion then becomes $\dot{q_{k}} = \frac{\partial H}{\partial p_{k}}$ and $-\dot{p_{k}} = \frac{\partial H}{\partial q_{k}}$
Chapter 8
Main Concepts
- The reduced mass is defined as $\mu = \frac{m_1 m_2}{m_1+m_2}$
- For two-body central force problems, we can write down the Lagrangian as $\frac{\mu}{2}(\dot{r}r^2\dot{\theta}^2)-U(r)$
- Via the Euler Lagrange equations and the coordinate transformation $r = \frac{1}{u}$ we find that $\frac{d^2u}{d\theta^2}+u = \frac{\mu}{l^2}\frac{1}{u^2}F(\frac{1}{u})$ where $l = \mu r^2\dot{\theta} = constant$
- For a gravitational potential $\frac{-k}{r}$, the equation of motion is $\frac{\alpha}{r} = 1+\epsilon \cos\theta$ where $\alpha = \frac{l^2}{\mu k}$ and $\epsilon = \sqrt{1+\frac{2El^2}{\mu k^2}}$
- The orbital period is related to the semi-major axis by the equation $\tau^2 = \frac{4\pi^2\mu}{k}a^3$
Chapter 9
Main Concepts
- $R = \frac{1}{M}\int \vec{r} dm $ is the center of mass (origin dependent)
- Equations of motion for composite objects can be reduced to following the point-like center of mass
- Elastic collisions have kinetic energy being conserved, while inelastic does not
- $\epsilon = \frac{|v_{2}-v_{1}|}{|u_{2}-u_{1}|}$ is coefficient of restitution. $\epsilon = 1$ is perfectly elastic
- Impulse is defined as $\int_{t_1}^{t_2} \vec{F} dt = \vec{P}$
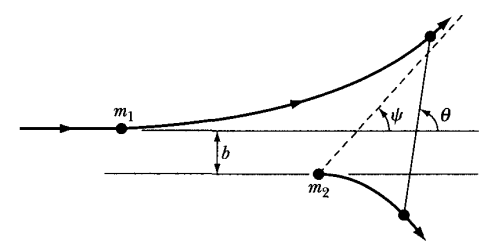
- b defines the impact parameter (the closest perpendicular distance of a particle approaching the target from infinity)
- The angular momentum then is $l = m_{1} u_{1} b$
- b defines the impact parameter (the closest perpendicular distance of a particle approaching the target from infinity)
- we define the differential cross section as $\sigma(\theta)$ to be the number of interactions per target divided by the number of incidnet particles per unit area
- $\sigma(\theta) d\Omega = \frac{dN}{I}$
- For an axial symmetry scattering problem, we have that $d\Omega = 2\pi \sin\theta d\theta$
- $\Delta \Theta = \int_{r_{min}}^{r_{max}} \frac{\frac{l}{r^2} dr}{\sqrt{2\mu[E-U-(\frac{l^2}{2\mu r^2})]}}$ denotes the deflected angle
- For Rutherford scattering, we integrate from b to infinity
- $\sigma(\theta) = \frac{k^2}{(4T_0)^2 \sin^{4}(\theta /2)}$
Chapter 10
Main Concepts
- Let a vector $\vec{A}$ denote any general vector
- $(\frac{d\vec{A}}{dt}) = (\frac{d\vec{A}}{dt})_{rot} + \vec{\omega} \times \vec{A}$
- The Force on an object in a rotating frame is given by $\vec{F}_{rot} = \vec{F}-m\ddot{R}-m\dot\omega\times \vec{r}- m\omega \times (\omega \times \vec{r}) - 2m \omega \times \vec{v}$
Chapter 11
Main Concepts
- $T_{rot} = \frac{1}{2}\Sigma_{\alpha} m_{\alpha} (\omega \times r)^2$
- This can be simplified to $TT_{rot} = \frac{1}{2}\Sigma_{i,j} I_{ij}\omega_{i}\omega_{j}$
- $I_{ij} = \Sigma_{a} m_{a} (\delta_{ij}\Sigma-{k} x_{a,k}^{2}-x_{\alpha,i}x_{\alpha,j})$ is called the moment of inertia tensor
- In the continuous case, we have that $I_{ij} = \int\rho(r)(\delta_{ij} \Sigma_{k} x_{k}^2 -x_{i}x_j)$
- diagonal terms are the moments of inertia and the off-diagonal terms are the products of inertia
- This can be simplified to $TT_{rot} = \frac{1}{2}\Sigma_{i,j} I_{ij}\omega_{i}\omega_{j}$
- Angular momentum now becomes $L_{i} = \Sigma_{j} I_{ij} \omega_{j}$
- Problems become greatly simplified if the moment of inertia tensor is diagonal. Then angular momentum aligns with axis of rotation
- By solving the eigenvalue problem of the tensor, you can calculate these principal axes
- The eigenvalues then become the entries of the new moment of inertia tensor
- Suppose that you want to know what the moment of inertia tensor becomes upon taking a different point as your origin. You can use the following generalization of the parallel axis theorem
- The new $I_{ij}$ in terms of the original $J_{ij}$ where $\vec{a}$ denotes the displacement vector is $I_{ij} = J_{ij}-M(a^2\delta_{ij}-a_{i}a_{j})$
- When the new axis is parallel to the old axis and you isolate yourself to a plane. We have that $I_{new} = I_{old}+Md^2$
- It it occasionally more convenient to have equations of motion in the body frame (ie. axes that align with the principal axes). Made up of 3 Euler angles
- The first Euler angle is called $\phi$ and denotes a counter clockwise rotation around the z axis in the fixed frame.
- Matrix of the form $\begin{pmatrix} \cos \phi && \sin\phi && 0 \\ -\sin\phi && \cos\phi && 0 \\ 0 && 0 && 1 \end{pmatrix}$
- The second Euler angle is called $\theta$ and is a counterclockwise rotation around the current x axis
- Matrix of the form $\begin{pmatrix} 1 && 0 && 0 \\ 0 && \cos\theta && \sin\theta \\ 0 && -\sin\theta && \cos\theta \end{pmatrix}$
- The last Euler angle is called $\phi$ and is the counterclockwise rotation around the current z axis
- Matrix of the form $\begin{pmatrix} \cos \psi && \sin\psi && 0 \\ -\sin\psi && \cos\psi && 0 \\ 0 && 0 && 1 \end{pmatrix}$
- Any vector can now be written in the body frame of reference $\vec{x_{new}} = \lambda_{\psi}\lambda_{\theta}\lambda_{\phi}x$
- In addition, we can rewrite the rotation vector components in terms of $\phi$, $\theta$ and $\psi$
- $\omega_1 = \dot{\phi}\sin\theta\sin\psi+\dot{\theta}\cos\psi$
- $\omega_2 = \dot{\phi}\sin\theta\cos\psi-\dot{\theta}\sin\psi$
- $\omega_1 = \dot{\phi}\cos\theta+\dot{\psi}$
- The first Euler angle is called $\phi$ and denotes a counter clockwise rotation around the z axis in the fixed frame.
Euler Equations
- Suppose that our Lagrangian is that of a free body (ie. V=0) and we only consider rotational kinetic energy
- We can express the Lagrangian as a function of $\psi$, $\phi$ and $\theta$. Taking these Euler angles as the generalized coordinates, one can show that
- $(I_{3}-I_{2})\omega_{2}\omega_{3}+I_{1}\dot{\omega_{1}} = 0$
- $(I_{1}-I_{3})\omega_{3}\omega_{1}+I_{2}\dot{\omega_{2}} = 0$
- $(I_{2}-I_{1})\omega_{1}\omega_{2}+I_{3}\dot{\omega_{3}} = 0$
Force Field
- One can calculate the torque on an object in a similar manner
- $(I_{3}-I_{2})\omega_{2}\omega_{3}+I_{1}\dot{\omega_{1}} = \tau_{1}$
- $(I_{1}-I_{3})\omega_{3}\omega_{1}+I_{2}\dot{\omega_{2}} = \tau_{2}$
- $(I_{2}-I_{1})\omega_{1}\omega_{2}+I_{3}\dot{\omega_{3}} = \tau_{3}$