High Energy Astrophysics

Scales

• Black holes are described by 3 parameters: Mass, spin, and charge
  • In practice, astrophysical black holes have no charge, since they are embedded in a plasma which “shorts out” the hole
• We can define some characteristic scales of black holes
  • $R_{s} = \frac{2GM}{c^{2}}$ is the Schwartzchild radius
  • $\Delta t_{LC} = \frac{R_{s}}{c}$ is the light crossing time (roughly the time needed to cross the black hole, up to a scale factor)
• How bright can be a black hole be?
  • We would want to convert all of the black hole’s mass into radiation in the relavent time scale
    • $L_{max} = \frac{Mc^{2}}{\frac{2GM}{c^{3}}} \approx \frac{c^{5}}{G} \approx 10^{59} \frac{erg}{s}$
      • For reference, supernovae are around $10^{52}$
    • What is the luminosity of the observable universe (excluding the blackholes)?
      • This is Fermi estimation problem: Find the mass of the sum, calculate the mass to energy conversion, and calculate the time needed for a photon to escape the center
        • The escape time is roughly a billion years, which gives a luminosity of around $10^{37}$
        • There are roughly $10^{10}$ stars in the universe. Assume all stars are like the sun
        • There are also roughly $10^{10}$ galaxies in the universe
        • Combining these gives that the luminosity of the universe is $10^{53}$
    • The point of this is that gravity is very efficient at converting mass to energy
  • If the black hole is moving close to the speed of light towards you (pileup of photons), then the observed luminosity can exceed this threshold
    • Gamma ray bursts (GRBs) are the prime example of this boosted luminosity

Eddington Limit

• Imagine that you have a star which is gravitationally bound and emits radiation.
  • These two forces oppose each other: gravity attracts to the center, while radiation pressure pushes the star boundary outwards
  • Larger stars have more mass, but they also tend to produce more radiation pressure
  • The Eddington limit is when these two forces balance each other
    • Define $\dot{m}$ as the accretion rate (gas falling onto a compact object or star)
    • The luminosity is $L = \frac{GM\dot{m}}{r}$, where $\frac{M}{r}$ is the compactness
      • The associated Eddington luminosity is an upper bound on the brightness of these objects (there are exceptions though)
• Let’s look at the simplest case: We have a fully ionized Hydrogen gas (plasma) accreting isotropically onto a star/ compact object
  • Electrons getting accelerated around protons produces radiation, which creates the outward pressure

Thomson Scattering

• Imagine a EM wave propagating along the $\hat{z}$ direction. This will oscillate an electron in a direction transverse to z (fix this direction to be x)
  • This oscillating generates the radiation
• Newton’s 2nd Law, and letting $E(z,t) = exp(i\omega t) \hat{x}$, the resulting motion is $x(t) = A exp(i\omega t)$ where $A = \frac{qE(z)}{m\omega^{2}}$
  • The cross section scales like $A^{2}$, which means that the cross section of the proton is roughly 1 million times smaller than the electron
    • $\frac{\sigma_{Tp}}{\sigma_{Te}} = \frac{m_{e}^{2}}{m_{p}^{2}}$
• The radiation force is defined as the energy flux times the cross section divided by the speed of light
• $F = \frac{L}{4\pi r^{2}} \rightarrow f_{rad} = \frac{\sigma_{T} L }{4\pi r^{2} c}$
• Setting the gravitational force (ignoring the electron mass) equal to the radiative force (ignoring the proton cross section) gives the target luminosity (re: Eddington Luminoosity) as $L_{edd} = \frac{4\pi c G M m_{p}}{\sigma_{T}}$
  • Setting the mass scale to that of the sun, we get that $L_{Edd} = 1.3E38 (\frac{M}{M_{*}}) \frac{ergs}{s}$
  • For a black hole, $L_{edd} = 1.5E45 M_{7} \frac{erg}{s}$ where $M_{7} = \frac{M}{1E7 M_{*}}$
• If we assume that the object is a perfect blackbody, we can define an effective temperature $L = 4\pi R^{2} \sigma_{B} T_{eff}^{4}$

Variability

• The acceleration is $\frac{GM}{r^2}$. Suppose that the radiation pressure suddenly vanished. How long would it take for the star to collapse?
  • Naively, one would say that $\frac{1}{2} a t_{dyn}^{2} = R \rightarrow t_{dyn} = \sqrt{\frac{2R^{3}}{GM}}$
    • Assuming that force at star radius is the same for all smaller radius
    • This is roughly $t_{dyn} = \frac{1}{\sqrt{G\rho}}$
  • $t_{dyn}$ sets the timescale for how quickly the luminosity of the star can change

Sense of Scale

• The above outlines the rough energies, wavelengths, frequencies and temperatures for each band of radiation

Atmospheric Attenuation

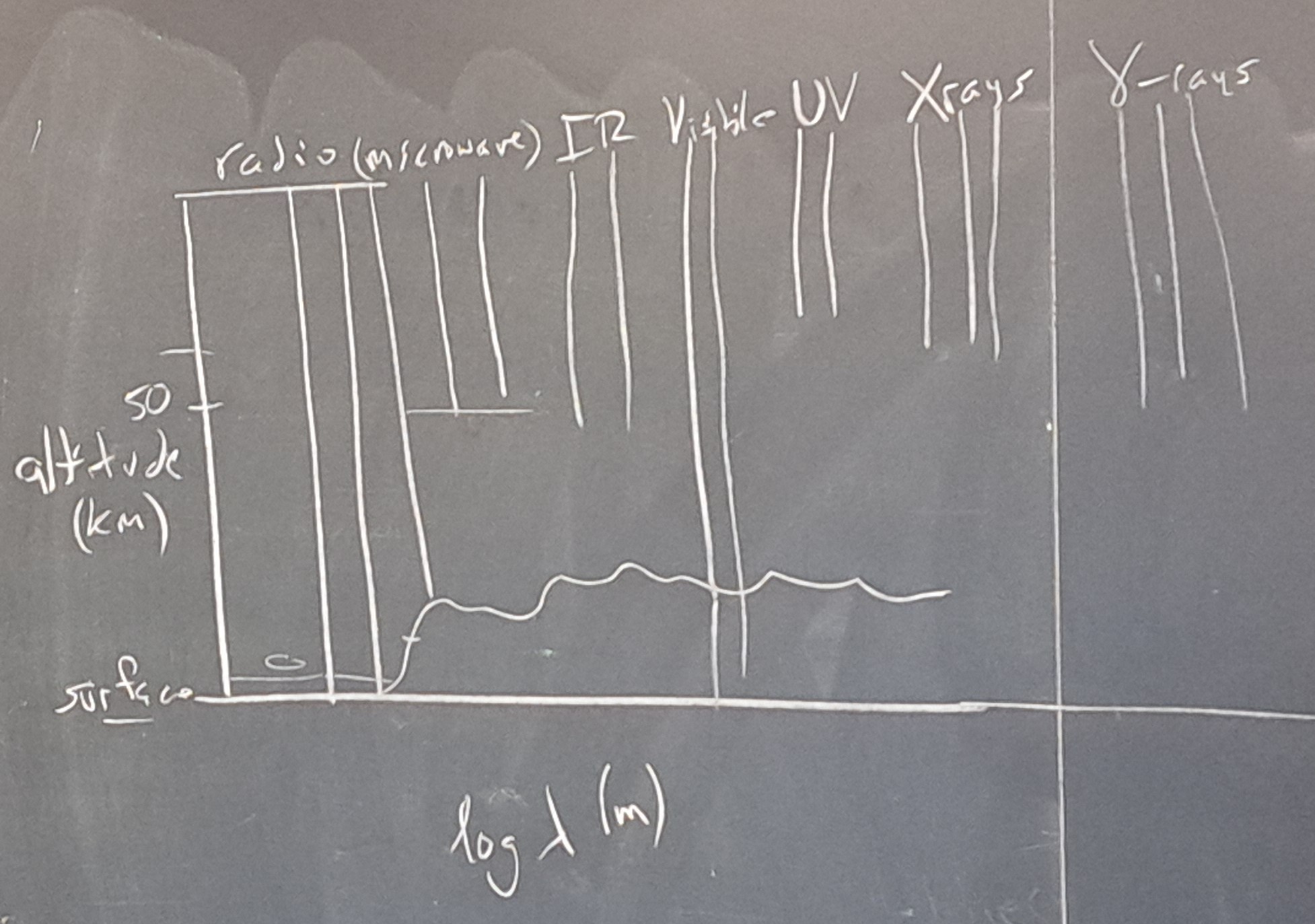
• Our atomsphere absorbs different amounts of radiation depending on the frequency
• This change is absorption is described by the opacity of the sky
• The above sets constraints on where expeiments/telescopes can be (radio and visible can be ground based, but other bands might demand high altitudes or be in space)

Intensities

• Define $I_{\nu} = \frac{dE}{dA dt d\nu d\Omega}$ as the frequency dependent brightness of a source
  • This is constant along rays in free space
    • Imagine that you have 2 detectors which are coaxial with seperation R and area $dA_{1}$ and $dA_{2}$ respectively
    • The energy change across each is $dE_{1} = I_{\nu_{1}} dA_{1} dt d\Omega_{1} d\nu_{1}$. Same for the 2nd detector
    • Solid angle is related to area via $d\Omega_{1} = \frac{dA_{2}}{R^{2}}$
    • The frequency and time crossing are the same
    • Use conservation of energy to see that the brightness is conserved
• Define the flux as $F_{\nu} = \int I_{\nu} \cos \theta d\Omega$
  • cosine modulation to account for when you don’t look at a source head on
  • You can recover the inverse square law by integrating over a small solid angle
• Define the pressure as $P_{\nu} = \frac{1}{c} \int I_{\nu} \cos^{2}(\theta) d\Omega$
  • Additional cosine arises from projecting onto the area of interest
• Define the energy density $u_{\nu}$ as $dE = u_{\nu}(\Omega) dV d\Omega d\nu$, or in terms of the brightness: $u_{\nu} = \frac{I_{\nu}}{c}$
• Define the mean intensity as $J_{\nu} = \frac{1}{4\pi} \int I_{\nu} d\Omega$

Particle acceleration

Cosmic Rays

• There exists cosmic rays which are protons of energies 1E21 eV
  • The LHC boosts protons to 1E13 eV
• When they hit the atmosphere, they create showers of high energy particles, which produce Cherenkov radiation cones in the air
• There is a hierachy of densities in our Universe:
  • On earth, the density of air is roughly 1E20 per cc
  • In the ISM, there is a density of 1E0 particles per cc
  • In the IGM, there is a density of 1E-6 per cc
• In the ISM and IGM, the mean free path $\lambda = \frac{1}{n \sigma}$ is very long, which lets particles get accelerated for a long time before getting scattered

Fermi Acceleration

• There are these objects called molecular clouds
  • These are objects in the ISM which form in slightly over-dense regions
  • They are called “star nurseries”
  • Point being, despite being made up of a bunch of particles, collectively the clouds have some average velocity in some direction
• There are a lot of these molecular clouds scattered around. Fermi realized that a particle could bounce off of these clouds and potentially gain these massive energies
  • This hinges on the fact that the velocity distribution of the clouds is assymetric
• A non-relativistic calculation of this phenomena:
  • Let $\Delta$ be the distance from the particle to the nearest cloud
  • Let $v$ and $V$ be the velocities of the particle and the cloud respectively
  • Let’s calculate the probability of a collision
    • The time until a head-on collision is $\tau_{u} = \frac{\Delta}{v+V}$
      • The velocities point in opposite directions
    • The time until a catch-up collision is $\tau_{c} = \frac{\Delta}{v-V}$
      • The velocities point in same direction
    • The probability of a head-on collision is $\frac{\frac{1}{\tau_{u}}}{\frac{1}{\tau_{u}}+\frac{1}{\tau_{c}}} = \frac{v+V}{2v}$
    • The probability of a catch-up collision is $P_{c} = \frac{v-V}{2v}$
  • What is the change in energy for each case?
    • Assume that the mass of the cloud is much larger than the particle. This is just an elastic collision
    • For a head-on collision: velocity after the collision is $v+2V$, hence $\Delta E_{h} = \frac{m}{2} (v+2V)^{2} -\frac{m}{2} v^{2}$
    • For a catch-up collision: velocity after the collision is $-v+2V$
  • What is the expected change is energy? Its $<\Delta E > = \Sigma_{i} P_{i} E_{i}$
    • Doing that calculation out gives $\frac{<\Delta E >}{E} = 4 (\frac{V}{v})^{2}$
      • This is a 2nd order process (b/c of the -2), which means it’s pretty inefficient
  • This Fermi acceleration is a general concept. There are “converging magnetic flows” where the “clouds” are always moving towards you. Hence you get a more efficient energy gain
  • Let $\frac{dE}{dt} \propto \nu < \Delta E>$, where $\nu$ is the frequency of collisions
    • For the molecular clouds, we see that $\frac{dE}{dt} = \alpha E$ for some characteristic $\alpha$ of the ISM
  • Let’s think of this problem in phase space, where our axes are E and x
    • $\frac{d N}{d t} = -\frac{\partial \phi_{s}}{\partial x} - \frac{\partial \phi_{e}}{\partial E} + \frac{\partial N}{\partial t}$
      • Think Stokes Theorem, where the flow on the boundary and the production of particles determines the change in the number of particles in some volume
    • The spatial flux is defined by $\phi_{s} = -D \frac{\partial N}{\partial x}$, where D is some diffusion constant
    • The energy flux is $\phi_{e} = \frac{N \Delta E}{\Delta t}$
    • We define some timescale $\tau$, which dictates how quickly particles leave the system (for instance, the Larmor radius grows so large so as to leave the system). This then gives that $\frac{\partial N}{\partial t} \approx -\frac{N}{\tau}$
    • For molecular clouds, D=0, and the system is in equillibrium, so $\frac{dN}{dt} = 0$
    • Solving for N yields $N(E) \approx N_{0} exp(-(1+\frac{1}{\alpha}{\tau}))$ where $\alpha = 4 \nu (\frac{V}{v})^{2}$
      • In log-log space, this is a straight line (re: a power law)

MHD (Magneto-hydrodynamics)

• We have Maxwell’s equations
  • $\nabla \cdot E = 4\pi \rho_{e}$
  • $\nabla \cdot B = 0$
  • $\nabla \times E = -\frac{1}{c} \frac{\partial B}{\partial t}$
  • $\nabla \times B = \frac{4\pi}{c} J \frac{1}{c} \frac{\partial E}{\partial t}$
• From Maxwell, we can derive charge conservation:
  • $\frac{\partial \rho_{e}}{\partial t} = \nabla \cdot J$
• We also make the ideal assumption (re: no resistivity)
  • This gives that there is no Lorentz force in the plasma (re: if there was a force, then due to no resistivity, the charges would rearrange themselves and short out the force)
  • Hence we have $\vec{E} \approx - \frac{\vec{v}}{c} \times \vec{B}$
• We add on the additional constraint of conservation of mass:
  • $\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{v}) = 0$
• Writing down momentum conservation gives:
  • $\rho \frac{d\vec{v}}{dt} = \rho \frac{\partial \vec{v}}{\partial t} + \rho (\vec{v} \cdot \nabla) \vec{v} = -\frac{\vec{B}}{4\pi} (\nabla \times \vec{B} - \frac{1}{c} \frac{\partial \vec{E}}{\partial t})$
    • In non-relativistic MHD, we can drop the $\frac{\partial E}{\partial t}$ term
• Suppose that you have some B field along the z axis, which experiences some sinusoidal peturbation in the x axis:
  • $\vec{B} = B_{0} \hat{z} + B_{A} exp(ikz- i\omega t) \hat{x}$
  • This could arise via neutron star quakes, or acretion disk turbulances
    • These quakes have some length scale $\lambda$, which modules the perturbation by $\sin(k_{y} y)$
  • The E field which gets created is $\vec{E} = \frac{ic}{\omega}(ikB_{a} \sin(k_{y}y) \hat{y} - k_{y} B_{A} \cos (k_{y} y) \hat{z}) exp(ikz-i\omega t)$
    • So this peturbation creates an E field along the magnetic field line, which can accelerate particles to relativistic speeds
    • This speed up is reduced due to synchrotron radiation

Acretion Disks

• We have gas around a object with a strong gravitational field
• Gravity can accelrate the charges, causing energy loses via radiation; angular momentum is preserved though
  • Radially, The balance of centrifugal acceleration and gravity causes the gas to gather into a disk
  • Vertically, the gravity gets balanced by the radiation pressure

Thin Disks

• A thin disk is defined as being thin in the z-axis (due to being cold and having low pressure)
  • The radial pressure gradient is negligible
• A thicker disk is hotter (hence larger pressure gradients)
• How does all the gas fall into the black hole when the portions of the disk have angular momentum?
  • There is a net flux of angular momentum out of the disk
    • Imagine a ring of gas of radial thickness dR at radius R. The angular momentum on the inside is $R\Omega(R)$, where $\Omega(R) = \frac{v_{\phi}}{r}$, and on the outside is $(R+dR)\Omega(R+dR)$
    • We imagine that there is some particle exchange from inside the disk to the outside, and vice versa
      • The torque due to the outflow is $\tau = \dot{M_{1}} (R+dR) R \Omega(R)$
      • The torque due to the inflow is $\tau = \dot{M_{2}} R(R+dR) R \Omega(R+dR)$
        • In short, the particles keep their old angular momentum as they cross the boundary
      • The inflow and outflow mass rate are the same ($\dot{M_{1}} = 2\pi R \rho(R) H \tilde{v}$).
        • H is the height of the disk. $\rho(z)$ is the density. $\tilde{v}$ is the average radial velocity of the disk
      • Hence, the net torque is $\tau = \dot{M_{1}} R(R+dR)(\Omega(R)-\Omega(R+dR)) = 2\pi R H \tilde{v} \rho(z) R(R+dR)(dR \Omega’(R))$
        • The kinematic viscosity is defined as $\nu = dR \tilde{v}$ (units of length squared over time)
        • Hence: $\tau = -2\pi \nu \epsilon R^{3} \Omega'$
      • There is a characteristic length and velocity scales in the problem (height of disk and speed of sound). You can encode this in the kinematic viscosity via $\nu = \alpha c_{s} H$, where $0 \leq \alpha \leq 1$
• Due to the viscosity of the gas, the friction generated causes the gas to radiate like a blackbody
• The mass flow of a ring is given by $R\frac{\partial \Epsilon}{\partial t} + \frac{\partial}{\partial R}(R\Epsilon v_{R}) = 0$
  • Imagine the mass flow at the inner and outer radii, then take the limit as dR goes to 0
  • $\Epsilon$ is the mass density of the ring, $v_{r}$ is the radial velocity
• Similarly, there is a flow of angular momentum: $R \frac{\partial}{\partial t}(\Epsilon R^{2} \Omega) + \frac{\partial}{\partial R}(R\Epsilon v_{r} R^{2}\Omega) = -\frac{1}{2\pi} \frac{\partial \tau_{out}}{\partial R}$
  • Same story: Take the difference between the inner and outer disks, and also add on the torques at the inner and outer rings
• Since the rings are Keplerian, we know that $\Omega = \frac{v}{R} \propto R^{-\frac{3}{2}}$
• We can combine mass and angular momentum conservation, along with the Keplerian ring assumption to calculate the radial velocity: $v_{r} = -\frac{3}{\Epsilon R^{\frac{1}{2}}} \frac{\partial}{\partial R}(v \Epsilon R^{\frac{1}{2}})$
• We can define $\dot{m} = 2\pi R \Epsilon (-v_{R})$

Thick Disks

• If the cooling is inefficient, or the mass accretion rate is too large, then disk has a tendency to become thick
• There are a lot of different regimes with funny names:
  • ADAF: advection-dominated accretion flow
  • RIAF: raidatively inefficient accretion flow
  • CDAF: convection dominated accretion flow
  • ADIOS: advection dominated inflow/outflow solution
    • You get like a quadropole movement in the flow, where one axis is an inflow while the other axis is an outflow
• Magnetic fields become more important, and the ideal MHD approximation breaks down

Analytic

• Assume that the angular velocity is now a function of z and R ($\Omega(z,R)$)
• For simplicity, assume that the radial velocity is much smaller than the angular velocity. the vertical velocity is also small
• Force balance gives $\frac{1}{\rho}\nabla P = -\nabla \Phi +\Omega^{2}\vec{R} = \vec{g_{eff}}$
• To simplify the analysis, let’s examine isobaric surfaces $\nabla P = 0$
• To further simplify the analysis, pretend that the z profile goes like $\pm R \tan \alpha $
• The potential takes the form $\Phi = -\frac{GM}{(R^{2}+z^{2})^{\frac{3}{2}}}$
  • Assume that z « R
• Doing the algebra and calculus gives $\Omega^{2}(R) = \frac{GM \cos \alpha}{R^{3}}$
  • This reduces to a Keplerian disk in the small $\alpha$ limit
  • Otherwise, the angular velocity is sub-Keplerian
• The radiation force becomes $\vec{F_{rad}} = -\frac{c}{\kappa \rho} \nabla P$
• Integrating the force over the surface area of the disk gives you the luminosity:
  • $L = \frac{4\pi c GM}{\kappa} -\frac{c}{\kappa} \int \nabla \cdot \Omega^{2} dV$
• Doing the integral, you get $L = L_{edd}(1+\sin \alpha \frac{r_{2}}{r_{1}})$
  • This can be super-Eddington!
  • This can explain how these super-massive black holes can be created in a Hubble time

Acretion Columns

• Imagine that the central accretor has some non-zero magnetic dipole moment.
• The B field for a non-zero dipole is $\vec{B} = \frac{3\hat{n}(\hat{n}\cdot\hat{m})-\vec{m}}{r^{3}}$
  • In our case, $\hat{m}$ is along the rotation axis of the acretor, and $\hat{n}$ denotes the direction we are measuring the field at
  • As a function of radius, assuming we are in the plane, we see that $B(R) = B_{0}(\frac{R_*}{R})^{3}$
• The pressure of the gas is given by $\frac{\rho GM}{R}$
• The magnetic pressure is given by $P = \frac{B^{2}}{2\mu_{0}}$
• The magnetic pressure has dynamical consequences once these pressures are comparable to each other
• The radius where this interchange happens defines this transition on behavior
• The gas, once below this radius, will flow along the magnetic field lines towards the poles of the acretor. This forms an accretion column

MHD

• We can describe our system as a function of pressure, velocity, and density at all x,y,z,t. These are not all conserved.
• We can construct a set of conserved variables from these: the total energy density (kinetic plus thermal), the momentum density and the density itself
• There are two pictures of flows that are useful
  • The Eulerian description imagines that you fix a box in space. You then look at the flow of stuff through the faces of the box and any stuff which gets generated in the box
  • The Lagrangian description follows a particular section of stuff around as a function of time and space
• With conservation of mass, we see that $\frac{\partial \rho}{\partial t} + \nabla \cdot (\rho \vec{v}) = 0$
  • Can derive by looking at the mass flow in a little box is size $\delta V = \delta x \delta y \delta z$
• With momentum conservation, we find that: $\frac{\partial}{\partial t}(\rho \vec{v}) + \nabla \cdot (\rho \vec{v}\vec{v}) = -\nabla \cdot \sigma + \vec{F_{b}}$
  • $\vec{v}\vec{v}$ and $\sigma$ are 3x3 matrices (re:tensors)
  • You can split the stress tensor into diagonal pressure components and off-diagonal shear components
• You can dot the above with $\vec{v}$ to get an power conservation law
• The 1st law of thermodynamics states:
  • $\frac{du}{dt} = T\frac{ds}{dt} + \frac{P}{\rho^{2}}\frac{d\rho}{dt}$
  • S is the entropy per unit mass

Bondi Accretion

• This describes the accretion of cold gas onto a central mass where the flow is primary in the radial direction
  • The interstellar medium (ISM) is such a cold gas
• Far away from the center accretor, the thermal energy density is given by $\rho c_{s}^{2}$. Define some radius $R_{a}$ where the thermal energy density equals the gravitational energy density
• Another relavent radii is $r_{s}$ (the sonic radius), where in infalling gas speed equals the sound speed
• Imagine that you have some steady radial flow:
  • From mass conservation, we know that $\frac{1}{r^{2}} \frac{d}{dr}(r^{2}\rho v) = 0$
    • The mass accretion rate is then defined as $\dot{M} = 4\pi r^{2} \rho (-v)$ (minus sign since the gas is always moving inwards)
  • From the momentum conservation, we have that $+\frac{\nabla P}{\rho}+ \frac{GM}{r^{3}} + v \frac{dv}{dr} = 0$
    • We assume an equation of state $P = D \rho^{\Gamma}$, which is representative of some ideal gas equation of state (or if $\Gamma=1$, it’s an isotherm)
  • If we define $c_{s}^{2} = \frac{dP}{d\rho}$, do some chain rule to change $\frac{dP}{d r} = \frac{\partial P}{\partial \rho}\frac{d \rho}{dr}$, and incorporate the mass continuity equation, we see that:
    • $\frac{1}{2}(1-\frac{c_{s}^{2}}{v^{2}}) \frac{d}{dr}(v^{2}) = -\frac{GM}{r^{2}}(1-\frac{2c_{s}^{2}r}{GM})$
    • This describes a transition from subsonic to supersonic speed
    • Radii which this occurs at is when $v(r_{s}) = c_{s}(r_{s})$, which translates to $r_{s} =frac{GM}{2c_{s}^{2}(r_{s})$
      • We know the sound speed and the density at infinity. We need to relate these parameters to the values at $r_{s}$
        • Look at energy conservation: $\frac{1}{2}v^{2} + \int \frac{dP}{\rho} - \frac{GM}{r} = constant$
          • Assuming that $\Gamma \neq 1$, we know that v=0 at $r=\infty$. This let’s you write the sound speed as a function of the boundary conditions. Remembering that $v = c_{s}$ at $r_{s}$, we see that:
            • $c_{s}(r_{s}) = c_{s}(\infty) (\frac{2}{5-3r})^{\frac{1}{2}}$
            • $\rho(r_{s}) = \rho(\infty) (\frac{c_{s}(r_{s})}{c_{s}(\infty)})^{\frac{2}{\Gamma-1}}$

Roche Lobes

• Most massive stars are in binary systems (~70%)
• We define the ratio between the two masses as $q = \frac{M_{2}}{M_{1}}$, where $M_{2} \leq M_{1}$
• In an inertial frame, the potential is just the sum due to each mass
• In a co-rotating frame, you can peg the masses in place, and add in some additional potential to model this rotation
  • For simplicity, we will only assume that the centrifugal force is relavent. Euler and Coreolis forces are small
• The centrifugal acceleration is $-\omega\ \times \omega \times r$, which means the potential is $\Phi(r) = -\frac{1}{2}(\vec{\omega}\times \vec{r})^{2}$ (just take the derivative w.r.t. r! to get back the force!)
• The relavent lengths of the system are:
  • The binary separation a: related to the period via Kepler’s Law: $4\pi^{2}a^{3} = G(M_{1}+M_{2})P_{orb}^{2}$
  • $R_{i}$ the average radii of each mass
  • $b_{i}$ the distance from the mass to the L1 Lagrange point
• The equipotentials of this system in the co-rotating frame looks like two lobes which meet at the Lagrange point L1
• Some heutristics for how these parameters evolve are:
  • $\frac{R_{2}}{a} 0.38+0.2 \log q$
  • $\frac{b_{1}}{a} = 0.5 -0.277 \log q$