ExperimentalTechniques

Taken from Experimental Techniques in Modern High-Energy Physics: by Hanagaki, Tanaka, Tomoto, Yamazaki

Why?

• Two basic categories of HEP experiments
  • Find any new particle by converting collision energy to particles
    • Done through finding resonances in the final state
  • Investigate the nature of a particular interaction
    • Done through precise measurements of other physical observables
• In theory, you work with a small number of states to keep problems tractable. Experimentally, you can get thousands of final states which you have to parse through
  • The number of particles goes as $ln \sqrt{s}$ where s is the square of the center of mass energy of the collision
    • This the angular density to go up, which create “jets” (ie. collimated bunches of particles)
      • You need to be able to distinguish particles within a jet from each other
  • Hence, you need to cover the full solid angle ($4\pi$) in order to get all the interactions (this is called a hermetic system)
• Because the cross-section goes as $\frac{1}{E^2}$, you need to compensate with a higher collision rate
  • This causes the background rate to increase because of “soft” collisions (ie. when particles don’t collide head-on). This is called pileup
  • You also have a tougher time taking in data
• You should also be able to reliably detect all sorts of stable particles (neutrinos, electrons, pions etc.) with sufficient resolution

Measurement

• We can’t observe elementary particle interacting directly, so we do indirect observation by tabulating various distributions

Cross Section and Luminosity

• Particles are not localized. They have some sort of spread to them (ie. they fuzzy)
  • To deal with this fuzziness, we pretend that the particle have some fixed cross sectional area in order to define the probability of hitting the target (ie. we pretend that particles are hard instead of fuzzy). This is called the cross section $\sigma$
• We define the instantaneous luminosity L as $L = \sigma f_{coll} \frac{n_{1}n_{2}}{a}$
  • $n_{1}$ and $n_{2}$ are the number of particles in beam 1 and beam 2, a is the area where the particles get injected in, and $f_{coll}$ is the frequency of collisions
  • The integrated luminosity is then $L_{int} = \int L dt$

$e^{+}e^{-}$ Example

• In order to identify an event, we first need to identify the type of final state particles (this is called particle identification or pid (Not the UNIX thing…))
  • For now, assume that we can identify particles with a confidence level
• Even if you identify particles, you need to think about what other debris there is in the detector
  • For instance, electrons emit soft photons (ie. low energy photons) due to their small mass. You can’t avoid those photons, and you can’t really differentiate them since their energy is so low
  • Hence, you compromise: you fold in the energy of these soft photons into the electron when you cannot distinguish them
• There is also the fact that most interactions are very forward. This means that most final states end up (near) parallel with the beams
  • Hence, since most detectors are not hermetic (since the beam has to enter from somewhere!) you can miss potential final states
• Therefore, suitable criterion to identify $e^{+}e^{-}$ events are
  • a pair of electron like particles that are sufficiently far enough from the injection site
  • No other significant energy deposits observed
  • Each electron has a large proportion of the beam energy
• You could also defined more relaxed conditions (called inclusive event selection) as
  • a pair of electron like particles that are sufficiently far enough from the injection site
  • Each electron has a large proportion of the beam energy
• The above criteria include other events, which can (hopefully) be removed in post
• Different selection criteria yield different acceptance A (ie. $A = \frac{N_{sel}}{N}$) and also different efficiencies $ie. \epsilon = \frac{N_{det\bigcap sel}}{N_{sel}}$
  • $N_{sel}$ is the number of events that passed the selection criteria, imposed on true four-momentum of particles
  • $N_{det\bigcap sel}$ denotes the number of events passing the selection criteron imposed in the measured momenta
• $N_{sig} = L_{int} \sigma A \epsilon = N_{obs}-N_{bkgd}$ is the total number of events that you take as your signal

Coordinate System for Hadron-Hadron Collisions

• The z-axis is along the beam line, with the positive direction pointing from beam A
• The x-axis points towards the center of the accelerator ring
• the y axis is choosen to form a right-handed coordinate system
• The transverse plane is the xy plane perpendicular to the beam direction
• The transverse momentum is $p_{T} = \sqrt{p_{x}^{2}+p_{y}^{2}} = p\sin \theta$ where $\theta$ is the polar angle in the xy plane
  • Typically, transverse momenta is characterized by $(p_{T}, \theta)$
  • This is used because $p_{T}$ is conserved in hadron-hadron collisions, but longitudinal momentum is not(b/c with partons, the $p_{parton} = x*p_{beam}$, and x is not the same for bot beam, which causes the center of mass frame of the two beams to be boosted with respect to the lab frame, hence the longitudial momentum gets squished, but the transverse remains unchanged)
• We defined the rapidity as $y = ln \frac{E+p_{z}}{m_{T}}$ where $m_{T} = \sqrt{m^{2}+p_{T}^{2}}$
  • Why?
    • $E\pm p_{z}$ is resistant to particle losses escaping the beam
    • Hence, we define a new coordinate that utilizes these more easily measurable quantities
    • rapidity is that differences in rapidity is preserved under a Lorentz boost
  • In the massless limit (which is a good enough approximation when your beam energy is 14 TeV!), you can define the pseudo-rapidity as $\eta = -\ln \tan (\frac{\theta}{2})$
• The phase space for a particle is defined as $d^{4}p\delta(p^{2}-m^{2}) = \frac{d^{3}p}{E} = \pi dydp_{T}^{2}$

Apparatus

• To make particles, you need to convert energy to mass. Hence, why high energy particles get smashed together
• In order to generate these high energies, we use at the LHC a sequence of increasingly little accelerators
• Once the particles get up to speed, they maintain their energy in the main synchrotron via RF (radio frequency) cavities which offsets the radiation losses. At the LHC, the bunch crossing occur every 25 ns
• bunch crossing refers to when two clusters of particles cross a small region
  • This is not the same as the collision: this refers to the particles that happen to interact with each other when the bunch crossing occurs
  • It’s possible that no collisions happen during a bunch crossing

Detectors

• We call the various expected ways to measure a particles existence “channels”
  • For instance, top quark annihilation event can yield
    • Two leptons
    • a lepton and a jet
    • all hadrons

Particle Signatures

• Electrons with high energy create electromagnetic showers upon hitting dense materials. They also undergo curved trajectories when in the magnetic spectrometer
• Photons also create electromagnetic showers, but, since they are neutral, don’t leave a curved path in the charged particle tracking system
• Muons, at the relavent energies, don’t leave EM showers. Hence, if you see long tracks, then you probably have a muon
• Hadrons: jets
• Neutrinos: No. Or less faciciously, you can’t detect them since the cross section is absurdly small. You can infer them from the missing transverse momentum

ATLAS

• Arbitrarily choosen since high level design is roughly the same for multi-purpose detectors
• You have a barrel with two end caps and a beam channel
• There are solenoid and toroid magnets to provide a magnetic field to measure particle momentum
• Surrounding the interaction point is the charged particle tracker which consists of pixel and strip silicon detectors
• the TRT (transition radiation tracker, not the drug) is a gas which produces ions when hit by electrons. These get drifted by the field in the cathode ray tubes up to a mesh of wires
  • You can then reverse engineer the path that a particle took
• Most particles penetrate the tracking detectors and then hit the electromagnetic calorimeter composed of a sandwich of lead and liquid argon (LAr)
  • Electrons and photons produce showers in the lead (ie. the absorber)
  • The electrons created by the showers deposit ini the LAr (ie. the detector)
• There is also a hadronic calorimeter outside the EM calorimeter. This is mostly just a plastic scintillator and iron sandwich (although this might change depending on the region in the calorimeter)
• The outermost layer is the muon spectrometer, which is a gas detector like TRT with a high timing resolution

Triggers

• The ATLAS detector generates 1 petabyt of data every second
  • 40 MHz bunch crossing at 2E8 channels (ie. output signals)
• This can be reduced by x100 with some cleverness, but it’s still too much
• You need to calculate on the fly if a piece of data is worth keeping or not. This process is called a “trigger”
  • ATLAS has two levels of triggers: L1 and HLT (higher level trigggers)

Statistics

Basic Definitions

• $\int P(x) dx = 1$
• $E[x] = \int x P(x) dx$
• $\sigma^{2} = E[x-E[x]]^2$

Uncertainty

• Every physical observable has two uncertainties associated with it
  • statistical uncertainties (ie. stochastic fluctuations in random processes)
  • Systematic uncertainties: fundamental deviations from ideals which creates errors

Distributions

Binomial

• $P(n) = \frac{N!}{n! (N-n)!} p^{n} (1-p)^{N-n}$
  • p is the “hit” probability
  • $\mu = Np$
  • $\sigma = Np(1-p)$
• For large N and small p, can approximate by a Poisson distribution with $\mu = Np$
• For large N and moderate p, can approximate by normal distribution

Poisson

• $P(n) = \frac{\mu^{n}e^{-\mu}}{n!}$
  • $\mu = mu$
  • $\sigma^{2} = \mu$
• For large $\mu$, the Poisson approaches a normal distribution

Normal

• $P(x) = \frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{(x-\mu)^{2}}{2\sigma^{2}})$
• $erf(x) = \frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{t^{2}} dx$
• FWHM: Full width half maximum = $2\sqrt{2 \ln 2 \sigma}$

Uniform

• $P(x) = \frac{1}{b-a}$
• $\mu = \frac{1}{2} (a+b)$
• $\sigma^{2} = \frac{1}{12}(b-a)^2$
• Useful in position measurements

Breit-Wigner

• $BW(x;M,\Gamma) = \frac{1}{\pi} \frac{\frac{\Gamma}{2}}{(M-x)^{2}+(\frac{\Gamma}{2})^{2}}$

Exponential

• Useful with unstable particles of lifetime of $\tau$
• $P(x) = \frac{1}{\tau}e ^{-\frac{x}{\tau}}$
• $\mu = \tau$
• $\sigma^{2} = \tau^{2}$

Chi Square

• Assuming N observables $x_{i}$ which are drawn from a series of normal distribution. We defined the chi-squared value as:
• $\chi^{2} = \Sigma_{i=1}^{n} \frac{(x_{i-\mu_{i}})^{2}}{\sigma_{i}^{2}}$
  • If the hypothesis is correct, then the variance should equal $(x-\mu)^{2}$. Hence, $\frac{\chi^{2}}{n}$ is expected to be 1

Figure of Merit

• figure of merit refers to how sensitive the measurement can be expected to be
• A common one is $\frac{N_{signal}}{\sqrt{N_{obs}}} = \frac{N_{signal}}{\sqrt{N_{signal}+N_{back}}}$
  • The square root arises since $\sigma = \sqrt{N_{obs}}$ shows the statistical uncertainty of total number of events
• If the background is large enough, you can drop the signal term in the bottom

Error Propagation

• Suppose that observable u is a function of several variables: $u = f(x_0,x_1…x_{n})$
• The errors in measuring each variable can add up and affect the error of the overall function. It follows that
  • $\sigma_{u}^{2} = \Sigma_{i=0}^{n} (\frac{\partial f}{\partial x_{i}})^{2} \sigma_{i}^{2}$

Maximum Likelihood

• We define the likelihood function as the probability to have a set of measurement $x_0,x_1…x_{n}$
  • $L(x;\theta) = \Pi_{i=1}^{n} f(x_{i};\theta)$
  • Where $\theta$ represents the unknown physical values
• One would expect that the real values of $\theta$ would maximize the likelihood function
• Hence, once can solve the equation $\frac{\partial L}{\partial \theta_{i}} = 0$ to find the most probable values of $\theta$
  • A little trick is to instead solve $\frac{\ln \partial L}{\partial \theta_{i}} = 0$, since the extrema don’t change
• This is where
  • $\hat{\mu} = \frac{1}{n}\Sigma_{i=1}^{n} x_{i}$
  • $s^{2} = \frac{n}{n-1}\hat{\sigma}^{2} = \frac{1}{n-1}\Sigma_{i=1}^{n} (x_{i}-\mu)^{2}$
    • This is where the stupid n-1 comes from!

Hypothesis Test

• A null hypothesis $H_{0}$ is the hypothesis under consideration
• The test hypothesis $H_{1}$ is the hypothesis that the null is conpared against
• In practice, $H_{1}$ is the hypothesis we would like to see, while $H_{0}$ is the hypothesis we would like to reject
• We define the ratio $\frac{L(H_{0})}{L(H_{1})}$ as the test statistic t. By Neyman-Pearson lemma, this is an optimal discriminator (Why? IDK. I’m sure I could understand if I read the proof, but that’s not relevant for what I’m doing)
• TBD

Detector Calibration

• Detector calibration is the process of converting ADC values to physical observables
  • Remember, ADC values are just numbers unless they can be correlated to observables

Detector Alignment

• A tracking device is aligned if all 6 degrees of freedom can be pinned down to a reasonable tolerance
• After the coarse placing of a device, one method to fine tune alignment is with charged particles
  • Suppose that you have a tracking algorithm that is agnostic to which layer is being aligned. You can compare the expected layer hit to the actual particle track, and then try and realign the layers so that the residual (ie. the difference between the two) goes to 0
  • In practice, this quicks gets tedious. Also, since there are millions of channels, using a layer agnostic tracking algorithm becomes nigh impossible
    • Instead, the normal track reconstruction algorithm is used with looser quality requirements in order to minimize the bias arising from the usage of hit information
    • The residual is also redefined as the sum of the residuals in each individual layer
• The alignment process occurred in a hierarchical manner (ie. align the big things together, then did down into the constituents)

Momentum Resolution

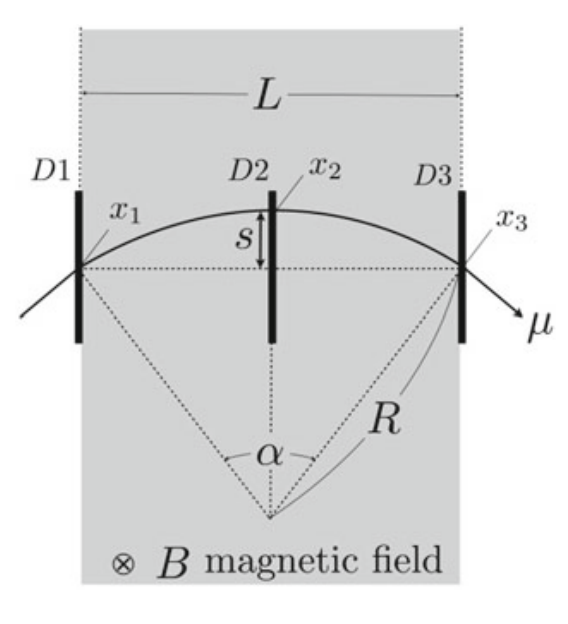
• Suppose a charge particle travels in a magnetic field B with the radius R. You can place 3 sensors along it’s path (D1, D2, D3) to detect its presence
• We define the sagitta as $s = R(1-\cos\frac{\alpha}{2})$
• The uncertainty in the momentum is given by
  • $\frac{\sigma_{PT}}{p_{T}} = \frac{\sigma_{x} p_{T}}{0.3 BL^{2}}\sqrt{\frac{720}{N+4}}$
    • N is the number of sensors along the arc
  • In light of the above, better resolution is achieved with more detectors in a wider space witha greater field strength
• Another calibration technique is to use the “world average value” of the invariant mass of well known particles like the Z boson in order to fine-tune scaling for each energy bin
  • There are some experimental trade-offs you have to make, like what particle to pick? Can you generate a large enough dataset? etc.

Energy Calibration

• Two main methods
  • Calibrate each cell/channel
  • Calibrate the energy of the particle incident to the calorimeter (ie. the energy of the shower after clustering)

Cell-By-Cell Calibration

• The goal of cell-by-cell is to find the relationship between the energy deposit and the ADC count for each channel
• muons are very common for this purpose since they behave as minimum ionising particles (MIPs) that deposit a constant energy per path length
  • Other particles either cause EM or hadronic showers, or don’t produce constant energy deposits
  • Muons deposit energy just by ionization loss, which causes the constant energy loss
  • Muons decaying from Z bosons are one of the cleanest samples you can get
    • They have no other particles near them
    • they have very high momentum (which means smaller scattering angle)
  • $J/\Phi \rightarrow \mu^{+}\mu^{-}$ is used as a lower momentum calibration source
  • Muons also come from cosmic rays, which are free and available everywhere in the world (except deep underground)
• Alternatively, one can send in test pulses (say light, or square waves) into each channel and then measure the response in order to make a correlation between input and output signals

Energy Clustering Calibration of EM Showers

• It’s hard to extrapolate muon data to higher energies
• There could be dead material in the detector
• To fix these issues, can utilize other auxiliary detectors to get a measurement of momentum of an electron, and the use a $\frac{E}{p}$ distribution to map onto energy
• You can measure decay of particles whose masses are precisely known
  • It’s kind of hard to find a reaction that can generate enough statistics though…
• Another difficulty is that it’s hard to produced good photon calibration reactions
  • To side step this, you typically calibrate on electrons, and then say that photons showers are roughly the same as electrons
    • The primary difference between the two is the starting shower depth (photons are deeper)
    • If you want greater precision, you can use MC simulations to dial in the truth depth of the photon shower
• After setting up an experiment, rarer processes can be used as validation (say $Z \rightarrow \mu^{+}\mu^{-}\gamma$)

Energy Clustering Calibration of Hadronic Showers

• Hadronic energy measurements are harder, since a lot of the energy gets “lost” due to nuclear interaction length
• Hadronic showers also have a larger variance due to ocassionally producing heavier particles like pions and stuff (EM is mostly just electrons and light)
• This discussion will be deferred to jet reconstruction, since it better fits there…

PID (Particle IDentification)

• Tracking refers to the reconstruction of a trajectory of a charged particle, or a track. It consists of 3 parts
  • measurement of the space hit points of the particles in the detector
  • the pattern recognition to the hit points to make a candidate track (ie. track finding)
  • the fitting for the candidate track to get a smooth track (best guess fo the true particle trajectory)
• In the real world, there are detector inefficiencies (which causes phantom hits, particles can penetrate multiple segments at once, multiple particles could deposit in the same segment)
  • To circumvent this, clustering is performs on the raw hits in order to group hits with similar characteristics together
    • Particle position can then be inferred from these clusters

Hit Clustering

• Ideally, one would set a (low) threshold for each channel to trigger a single hit
• We don’t live in an ideal world, as much as physicists love their spherical cows
  • There can be dead channels, which don’t register anything
  • There can also be noisy channels, which register garbage or are constantly on
• For dead channels, we can pretend that it registered a hit if the surrounding channels are registered a hit
• For noisy channels, we could just mask them out (ie. ignore them)
  • One could also demand that channels adjacent to the noisy one registers a hit

Hit Point Determination

• Given a series of hits, can take a weighted average w.r.t. the measured charge to find the most likely position
• Older detectors utilized wires to glean this information. Needed to offset wires and a stereo angle in order to extend to higher dimensions
  • Stereo angle of 90 degrees very uncommon since geometric constraints typically place readout electronics at one end of detector
  • This reduces positional resolution along the wire direction

Tracking Finding

• In the good ol’ days, we used our eyes to track particle through bubble chambers and we liked it!
• Modern detectors necessitate computer usage to keep up with data acquisition rate
• In either case, once a reconstructed track is produced, a chi-squared analysis is used to determine the goodness of the reconstruction

Local Method

• You greedily match tracks until you can’t any more, then repeat
• You could start inside out, or outside in
  • inside out has a higher number of potential tracks, so you use a lot more CPU time and exhasutively search the parameter space
  • outside in is faster due to the smaller number of potential tracks
    • It also allows reconstruction of tracks from a secondary vertex more easily
  • ATLAS does both of these things in parallel

Global Methods

• Histogramming: You can make a histogram of your hits with respect to some coordinate system such that you are sampling along a constant cooridinate. You can then run a peak finding algorithm to determinte the tracks
• Hough Transform: the classical version is mapping a writing the equation of a line in polar coordinates. Multiple points a long a line will produce marginally different sine waves, but those waves will overlap at some $r_{0}, \theta_{0}$ value which defines the line of best fit
  • This idea can be extended to other, more relevant paths, such as helices, which are pertinent to identifying charged particle motion

Vertex Finding

• The collision point if often called the primary vertex
• Decays can produce secondary vertices
• Intersecting tracks yield vertices
• Doing a best-fit analysis allows one to deduce the most likely vertices

Jet Identification

• If it looks collimated and is away from other stuff, it may be a jet related to an underlying parton
• Jet algorithms need to have the following properties
  • The algorithm has to be independent of the type/count of particles
  • The Algorithm should be able to reconstruct high momentum partons
  • The algorithm should be insensitive to soft emmissions

Cone Based

• Moves around a window of jet area defined as a circle in $\eta-\theta$ space with dimensions $\delta r, \delta \eta, \delta \theta$
• We iteratively find an energetic cluster such that $\delta r = \sqrt{\delta \eta ^{2} \delta \phi^{2}} < R$ for some cone radius R
  • We also demand that the transverse momentum is maximized
• This allows one to identify hard jets
• Unidentified clusters get thrown away

Cluster Based

• All particles, no matter how ghostly, gets assign to a jet
• If a particle is not assigned a jet, it gets added to the closest one according to some distance metric