Compilers

Referencing “Modern Compiler Implementation in ML” by Andrew W. Appel.

Lexical Analysis

• This refers to breaking up the input source code into individual words/tokens
• A “token” is a sequence of characters that can be treated as a unit in the grammer of a programming language
• Some common tokens which are typical in programming languages:
  • ID: think names of any kind (variable, function classes etc.)
  • NUM: Think integers
  • REAL: Think floating point
  • RESERVED: Words which are reserved in the programming language. “If” is a typical one
    • These reserved words cannot be used as identifiers (ID)
• macros and preprocessor directives are done prior to lexing
  • Only “weak” languages require a macro preprocessor (what does that mean?)
• Some of these token hae semantic values attached to them (think identifiers and literals), which give additional information

Regular Expressions

• You could describe the lexical rules of a programming language in a normal language
  • That’s very verbose and not precise
• A language can be though of as a set of strings
• A string is a finite sequence of symbols
• the symbols are drawn from a finite alphabet
• A language can be a finite or infinite set
  • The Pascal language is an infinite set, since it includes all possible Pascal programs
  • The language of C reserved words is the set of all alphabetic strings that cannot be used as identifiiers in the C programming language
• In this viewpoint, we just need to figure out if a given string is within the language set or not
• Regular expressions provide a compact notation to represent a set of strings
  • Symbol: each symbol the alphabet of the language, the regular expression $\mathbf{a}$ denotes the language containing just the string “a”
  • Alternation: given two regular expressions M and N, the alternation operator ("|") creates a new regular expression $M | N$. A string is in this new language if it was in language M or language N
  • Concatenation: Given regular expressions M and N, $M\dot N$ creates a new regular expression. A string is in $M \dot N$ if said string the concatenation of any two strings in the sub languages (so $(a|b) \dot a$ is the language of strings “aa” and “ba”)
  • $\epsilon$ represents the languages whose only elements is the empty string
  • Repetition: Given a regular expression M, the Kleene closure M* defines a new language. A string is in M* if said string is a concatenation of zero or more strings, all of which are in M (so $((a|b)\dot a)*$ is an infinite set of strings $("", “aa”, “ba”,“aaaa”,“baaa”, “aaba”, …)$)
• The above are the base operations. You can make some notational short hand:
  • $[abcd] = (a| b|c|d )$
  • $[b-g] = [bcdefg]$
  • $M? = (M| \epsilon)$
  • $M+ = (M\cdot M*)$
• There are also some convenience things:
  • a “.” represents any single character except newline
  • A string wrapped in quotes (re: “a.+*” stands for itself literally)
• Using the above, we can write some common tokens as:

Regex	Tokens
if	$250
[a-z][a-z0-9]*	(ID)
[0-9]+	(NUM)
([0-9]+"."[0-9]*)	([0-9]*"."[0-9]+)

• A given lexical specification is complete if it always matches some initial substring of the input
  • Can achieve this by having a rule that matches any single character
• There is some ambiguity in these rules, like what if there are multiple matches? Lex uses two disambiguation rules
  • Accept the longest match which satisfies the regex rules
  • If multiple regular expressions match a longest substring, then the first regular expression determines it’s type
    • This implies that the order you list the regular expressions in matters
  • As an example, “if8” will get matched to an identifier, while “if” gets matched to the IF token

Deterministic Finite Automata (DFA)

• Need to be able to implement regex in a computer program. One representation which lends itself well to this is a finite automaton
• Consists of a finite set of states, along which edges (labelled by a symbol) which transitions between each state
• One state is denoted as the start state, while there can be multiple states which are final states (re: a regex expression needs to end on one of these)
• In a deterministic finite automaton (DFA), no two edges leaving from the same state are labelled with the same symbol
  • a DFA can take in a string, and either accept or reject said string. From the start state, each character in the string induces a transition to some other state. If there is no valid transition available, or if after consuming the string, the DFA is not in a designated final state, then the string is rejected

• You can convert this graphical representation of the DFA into a transition matrix
  • This is a 2D array which is subscripted by the state number (re: all possible states) and the input character (re: all of the alphabet of the language)
    • Each entry in the matrix tells you which state you need to jump to
  • There is a “dead” state that just loops to itself on all characters (used to encode the absence of an edge)
• You also need a “finality” array, which maps state number to tokens
• If you want the longest match for a given input string, you also need to keep track of the last final state the DFA was in, as well as the associated character position

Nondeterministic Finite Automata (NFA)

• Unlike DFAs, NFAs can have edges which share the same symbol. In addition, special $\epsilon$ edges can be traversed without consuming any input
  • The non-determinism comes from the fact that you need to pick which branch you go down

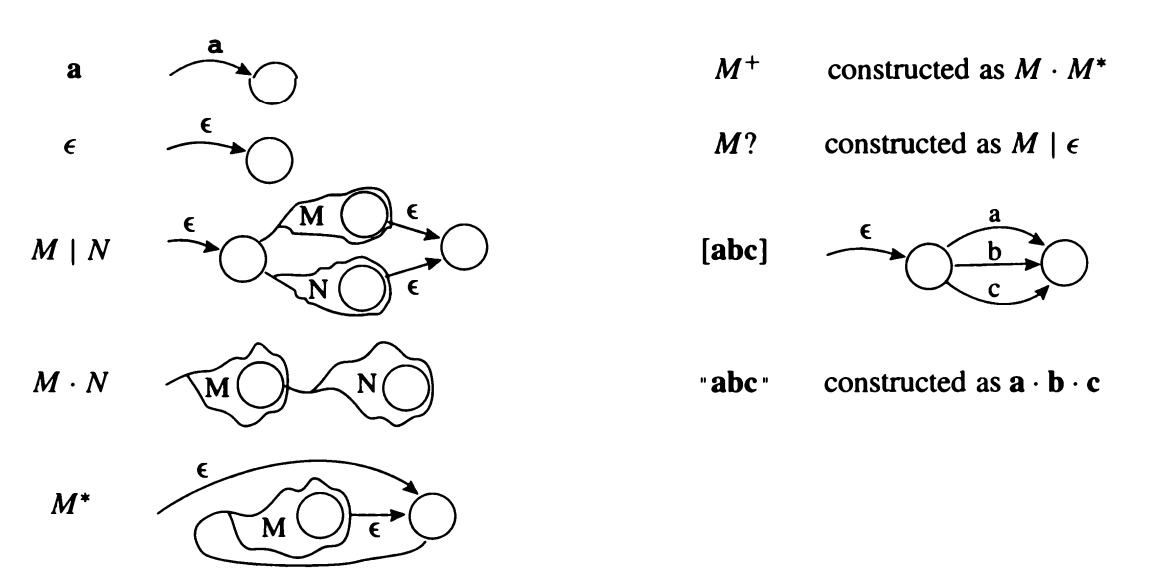
• It’s easy to convert a regex into a NFA. Just follow the above rules. At the end, you should end up with some NFA with a tail and a head
  • Each symbol gets converted into a tail (re: transition) and a head (re: a state)
    • Same for an $\epsilon$ edge
  • Concatenations are just chains
  • Alternations are just split paths with an epsilon edge buffer
  • Repetition is just a feedback loop
• This is not necessarily the most efficient realization of said regular expression, but it works
• Each regular expression is either a primitive (a single symbol or $\epsilon$) or it is made from smaller expressions. Ditto for NFAs
• Going from a NFA to DFA is harder
  • In order to get the longest match, you need to be able to traverse all of the parallel $\epsilon$ edges at a given node (This applies recursively)
    • This describes the notion of an $\epsilon$-closure
  • Let edge(s,c) be the set of all NFA states reachable by following a single edge with label c from state s
  • For a set of states S, closure(S) is the set of states that can be reached from a state in S without consuming any of the input (re: you cross all the reachable $\epsilon$ edges)
    • This can be represented mathematically. closure(S) is the smallest set T such that $T = S \cup (\cup_{s\in T} edge(s, \epsilon)) $
    • T can be calculated in a straight forward manner: while $T_{new} \neq T$, let $T_{new} = T \cup (\cup_{s\in T} edge(s, \epsilon))$
      • This converges since T can only grow every iteration. There is a finite number of states, so the algorithm must terminate. If the cardinality doesn’t grow ($T_{new}= T$), this means that T includes $(\cup_{s\in T} edge(s, \epsilon))$
  • Suppose that you have a set d of NFA states you need to visit. Define a function DFAedge(d,c) where closure( $\cup_{s\in d}$ edge(s,c))
    • Can think of this as traversing the edges associated with a character, and then traversing all of the epsilons
  • You can simulate an NFA via the following algorithm
    • let d be the closure of your start state $s_{1}$
    • for each character in you input string, calculate DFAedge(d,$c_{i}$), then update you set d

• The above outlines how to construct a DFA using closures and DFAedge
  • $\Sigma$ denotes the alphabet of the language
  • In words, you start with the set generated by the closure of the start state. Iterate through this set. If a character matches one of the edges, check if the connecting state is already in the set. If it is, set that the associated element in the transition matrix to the next state. Otherwise, append the state to the queue, and set the transition matrix element. Do this until you have gone through all of the states
  • This algorithm doesn’t reach unreachable states, which prevents exponential blowups
  • This is not an optimal automaton