Particle Astrophysics & Cosmology

Compilation of notes for Astrophysics and Cosmology class for Spring 2023.

Special Relativity
- Spacetime Diagrams
- Metrics
Classical Cosmology
Non-Euclidean Geometry
Early Universe Physics
Particle Physics Theory
Classical and Quantum Theory of the Scalar Field
Inflationary cosmology revisited, and structure formation
The Cosmic Microwave Background (CMB)
- Observations of the CMB
- Measuring CMB
  - Correlation Function
  - CMB Acoustic Oscillations
Primordial Black Holes and Hawking Radiation
- Application to Inflation
  - Polarized CMB
Neutrinos

Special Relativity

Spacetime Diagrams

Simplest visualization is 2D plot. One axis is ct, the other is x (ct is for consistent dimensions, could also do x/c to measure in units of time).
The true diagram plots the vector $<ct,x,y,z>$ in a 4-dimensional manifold. Each one of these vectors is an event in spacetime

Worldline

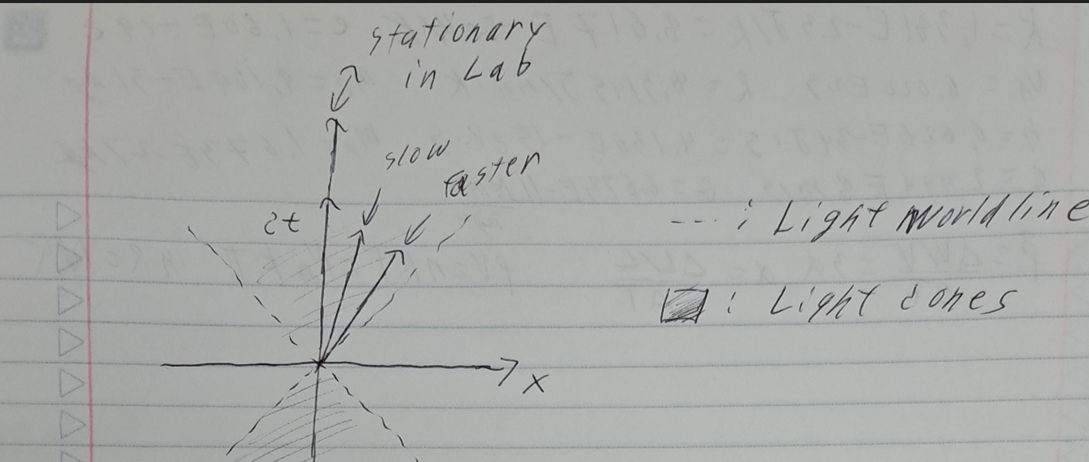
SpacetimeDiagram

Worldline denotes our trajectory through spacetime
If you are stationary at x=0, then you get a vertical line at x = 0
If you walk to the right, then your x coordinate increases
A light beam moves along the $45 \degree$ lines (either in 1st or 2nd quadrant)
The faster you go, the closer you slope gets to unity (ie. light speed)
The future light cone denotes the area above the x axis between the light worldlines
The past light cone denotes the area below the x axis between the light worldlines

Inertial Frames

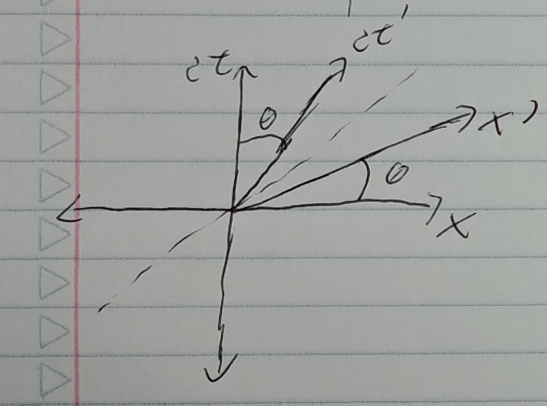
How to Draw X axis

Consider two frames, one stationary, the other strapped to a rocket (the prime frame). Observer has their own clocks and rulers
The events measured by the rocket are given by $<ct^{’},x^{’},y^{’},z^{’}>$, and the events in the lab are given by $<ct,x,y,z>$. The distinction is purely for bookkeeping.
Assume that the rocket moves with velocity v relative to lab frame
- Draw the worldline of the rocket in the lab frame. This is the axis ct’ of the rocket frame
  - This makes sense. The rocket observer is always at $x^{’}=0$ if they are not moving in their frame. So it makes sense that the worldline is the $ct^{’}$ axis
- To draw the x’ axis, take the angle between ct’ and ct axis. Transfer this axis to a positive angle from the x axis. This is the x’ axis

Postulates of SR

Light has a constant speed of c
Light moves isotropically for all observers
Imagine in the lab frame, you have a point source of light. Then $x = ct \rightarrow (ct)^{2} = x^{2}+y^{2}+z^{2}$
Similarly, in the rocket frame, you get $x^{’} = ct^{’} \rightarrow (ct^{’})^{2} = x’^{2}+y’^{2}+z’^{2}$
We can combine the above to get:
$(ct^{’})^{2} - x’^{2}+y’^{2}+z’^{2} = (ct)^{2} - x^{2}+y^{2}+z^{2} = s^{2}$
- $s$ is invariant between reference frames and holds true for any event, not just light. Called the interval and is used to define distance in spacetime
- can also be defined as $-s^{2} = x^{2}+y^{2}+z^{2}-c^{2}t^{2}$

Deriving Time Dilation from diagrams

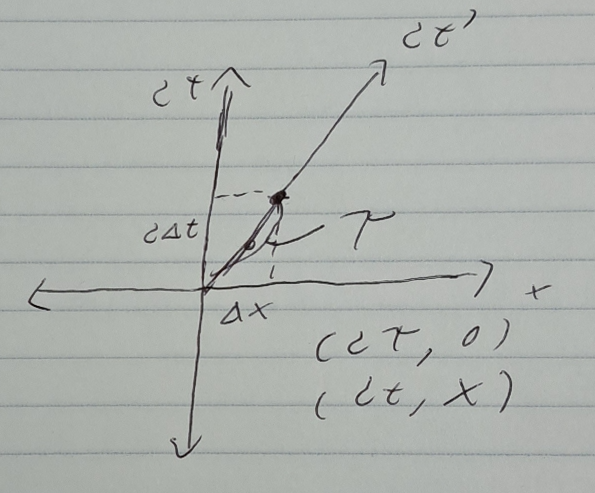
Time Dilation Diagram

Suppose $\Delta x$ and $\Delta t$ displacements occur lab frame. This corresponds to a displacement of $\tau$ in rocket frame
- rocket: $(c\tau,0)$, lab: $(ct,x)$
- The $s^{2}$ must be the same in both frames:
  - $c^{2}t^{2}-x^{2} = c^{2}\tau^{2}$. Rearrange as needed to get time dilation

Deriving Doppler Shift from Diagram

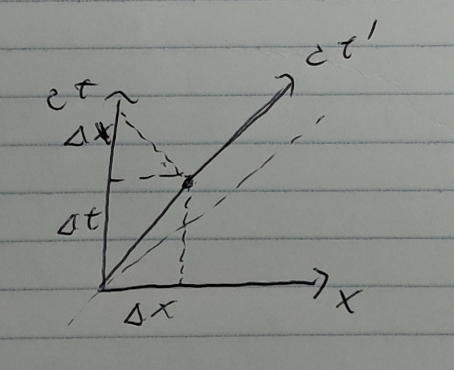
Doppler Shift Spacetime

The rocket is travelling at a velocity v. The rocket shots a light beam back to the lab frame (a 45 degree ray aimed at ct axis that starts at the end of the rocket trajectory)
- The rocket has displacements $c \Delta t$ and $\Delta x = \beta c \Delta t$. In the rocket frame, this displacement is $\tau$.
- The round trip time measured by the lab is:
- $\Delta t_{r} = c\Delta t + \Delta x = c\Delta t + \beta c \Delta t \rightarrow \Delta t_{r} = \Delta t (1+\beta)$
  - You add $\Delta x$ because this is the elasped time that the light takes to reach x=0 from the rocket
  - Substitute $\Delta t$ with $\Tau$ using invariance of $s^{2}$ and simplify
  - $\Delta t_{r} = \sqrt{\frac{1-\beta}{1+\beta}}$
- $\tau \propto \frac{1}{\nu_{e}}$ and $\Delta t_{r} \propto \frac{1}{\nu_{r}}$, where $\nu_{e}$ is the emmision frequency and $\nu_{e}$ is the receiver frequency
- In terms of wavelength:
  - $\lambda_{r} = \lambda_{e}\sqrt{\frac{1\pm \beta}{1\mp \beta}}$ (plus and minus depends on relative velocity direction)

Metrics

Metric tensor (SR)

$ds^{2} = c^{2}dt^{2}-(dx^{2}+dy^{2}+dz^{2})$
metric denoted as $\eta_{\mu\nu}$ or $g_{\mu \nu}$
- A diagonal matrix whose 0,0 component is 1 and other elements is -1 (convention dependent)

Covariant versus contravariant vectors

$dx^{\mu} = (cdt,dx,dy,dz)$
contravariant (upper index)
covariant (lower index)
Can transform contravariant to covariant:
- $dx_{\mu} = \eta_{\mu\nu}dx^{\mu}$
- Uses Einstein summation convention: upper and lower indexes of the same variable are implicitly summed along that index
$ds^{2} = \eta_{\mu\nu}dx^{\mu}dx^{\nu}$
- This is a scalar (same in all reference frames)
- Definition of distance of a 4D spacetime vector
Contravariant: $X^{\mu} = (ct, \vec{x})$
Covariant: $X^{\mu} = (ct, -\vec{x})$
$X_{\mu}X^{\mu} = c^{2}t^{2}-|\vec{x}|^{2}$

Metric in Spherical Coordinates

$ds^{2} = c^{2}dt^{2}-(dr^{2}+r^{2}[d\theta^{2}+sin^{2}\theta d\phi^{2}])$
$dx^{\mu} = (cdt,dr,d\theta,d\phi)$

4-Momentum

$P^{\mu} = (\frac{E}{c},\vec{p})$
- $E = \gamma mc^{2}$
- $\vec{p} = \gamma m\vec{v}$
$P^{\mu}p_{\mu} = (\frac{E}{c})^{2}-|\vec{p}|^{2} = (mc)^{2}$
- c =1 because it is quite tedious to haul around. Can add in later
- m = 0 for a photon: $E = p$
- For a particle of mass m at rest: $E=m$

Example

1 pc = 3.26 ly
- $1\ ly\approx 10^{18}$
Uniformly spread throughout the universe is DM
$DM+DM\rightarrow \bar{p}+\bar{D}$
- $DM$ refers to a dark matter particle
- $\bar{p}$ is an antiproton
- $\bar{D}$ is an antideuteron (deuteron = heavy hydrogen ie. 1 proton and 1 neutron)
Cosmic Ray ISM: $p+p\rightarrow p+p+\bar{p}+p$
$p+p\rightarrow p+p+\bar{p}+p+\bar{n}+n$
- Rarely $\bar{p}+\bar{n} \rightarrow \bar{D}$
How much energy does the cosmic ray need to make a $\bar{p}p$ pair?
Consider two frames (the lab frame and the center of mass frame):
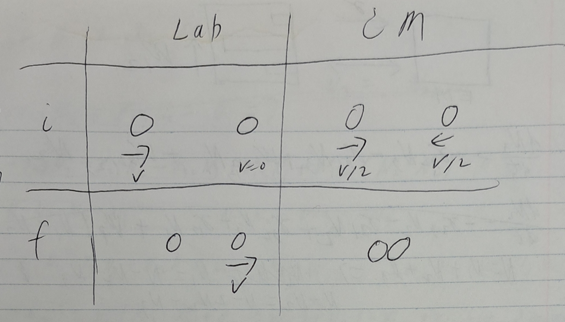
- The lab frame: The photons collide and scatter off
  - Let only 1 photon be moving and the other be at rest in the lab frame
  - $P^{\mu}_{lab,i1} = (E,P)$
  - $P^{\mu}_{lab,i2} = (m,0)$
  - $P^{\mu}_{T} = (E+m,P)$
- The CM frame: At threshold energy, the protons collide and are not moving
  - $P^{\mu}_{CM,f} = (4m,0)$
- Conservation of momentum states $P^{\mu}P_{\mu}$ is the same before and after the collision in both frames
- The final momentum is the same in both the lab and the CM frame
- Comparing invariants: $E^{2}+2Em+m^{2}-P^{2} = 16m^{2}$
  - Rearrange and recalling that $E^{2}-P^{2}=m^{2}$, you get
    - E = 7m
    - Recall $E = K+m \rightarrow K = 6mc^{2}\approx 6\ GeV$
$F(E) \propto E^{-2.7}$
- units of $\frac{particles}{m^{2}\cdot sr \cdot s \cdot GeV}$
- The antiduteron requires a significantly larger amount of energy to be produced from cosmic rays (HW problem)
- Because of the cosmic background spectrum, natural background of antideuterons from cosmic ray at low energy is pretty small
- Hence, low energy antideuterons are a “smoking gun* for dark matter because of this low background (below $K\leq 200 MeV$ is about the energy predicted)

Classical Cosmology

The Cosmological Principle

Our position in space and time is not special
Local physics does not differ markedly from those made by other observers elsewhere in the universe
- homogenous: all observers see the same thing
- isotropic: each observer sees the same thing regardless of direction
If you zoom out enough ($\geq$ 100 Mpc), then the universe looks isotropic

Comoving Coordinates

A Comoving Observer who carries their clock with them (reading proper time) AND also carries their coordinate location with themselves
an “event” is characterized by a comoving observer AND their time
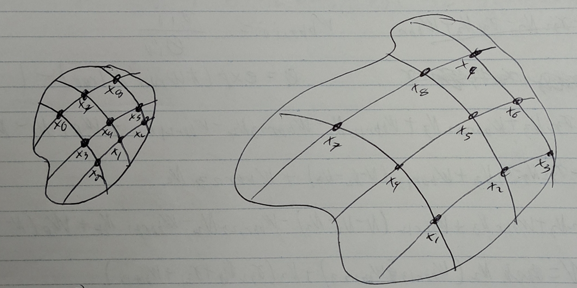
Draw a coordinate system on the surface of an inflated balloon. Let each intersection be a comoving observer (ie. each observer denotes a position on the sphere). All the clocks are synchronized to time $t_{1}$
At a later time, after the balloon has expanded, we see that the distance between each observer has increased; however, each observer maintains their coordinate (ie. coordinate distance is NOT the same as physical distance)
- Define a particular observer as (0,0)
- Define a scale factor $a(t)$ to denote the rate of expansion of the balloon
- Let $d_{1} = a(t_{1})\vec{s}$, where $d_{1}$ is the physical distance at time $t_{1}$ and $\vec{s}$ is the coordinate distance
- Let $d_{2} = a(t_{2})\vec{s}$ at time $t_{2}$
- Define $\vec{v} = lim_{t_{2}\rightarrow t_{1}}\frac{d_{2}-d_{1}}{t_{2}-t_{1}}=\frac{a_{2}-a_{1}}{t_{2}-t_{1}}\vec{s} = \dot{a}(t_{1})\vec{s} = \frac{\dot{a}}{a}a\vec{s}$

Hubble’s Law

The above yields Hubble’s Law: $\vec{v} = H\vec{d}$ with $H = \frac{\dot{a}}{a}$
Hubble Flow: the velocity of comoving observers due to the expansion of the universe
Hubble’s Law implies homogeneity
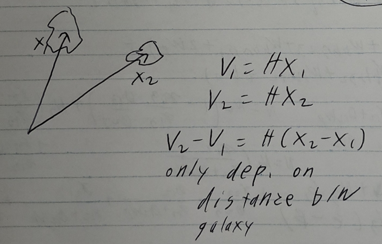
- Imagine two galaxies at positions $x_{1}$ and $x_{2}$. Hubble’s law states:
  - $\vec{v_{1}} = H\vec{x_{1}}$
  - $\vec{v_{2}} = H\vec{x_{2}}$
- Subtract the two from each other demonstrates homogeneity
- the velocity between galaxies is independent of where you are in space (ie. it only depends on the relative distance between galaxies)
- $H_{0}=\frac{\dot{a}(t_{0})}{a(t_{0})}$ is the Hubble constant measured “locally” and measured between galaxies that are “not to distant”

Wavelength relation to scale factor

Consider 2 galaxies on different comoving coordinates
- The wavelength at one galaxy is $\lambda(t)$
- The wavelength of the first galaxy as measured by the second galaxy is
  - $\lambda(t+\delta t)=\lambda(t)(1+\frac{v}{c})$
  - $\delta t = \frac{l}{c}$ where $l$ is the distance between the galaxies
  - $v=Hl=\frac{\dot{a}}{a}\delta t$
    - Plug this into the wavelength as observed by the second galaxy, rearrange and divide by $\delta t$ to eventually get
    - $\frac{\dot{\lambda}}{\lambda}=\frac{\dot{a}}{a}\rightarrow \lambda \propto a$
- An important quantity is $\frac{\lambda(t_{o})}{\lambda(t_{e})}=\frac{\dot{a}(t_{o})}{a(t_{e})}=1+Z$
  - $Z=\frac{\lambda(t_{0})-\lambda(t_{e})}{\lambda(t_{e})}=\frac{v}{c}$. THis is called the redshift.
  - You can have $Z\geq 1$ since $v\leq c$ only in inertial frames of reference (ie. the universe expands faster than c)

Luminosity Distance (L)

Luminosity: $L=\frac{erg}{s}$
Flux $F=\frac{erg}{s*cm^{2}}=\frac{L}{4\pi D_{L}^{2}}$
The luminosity distance is defined as $D_{L}=\sqrt{\frac{L}{4\pi F}}$
$D_{L} = D_{L}(Z,args)$ where $args$ are relevant cosmological parameters.

Non-Euclidean Geometry

Flat space denotes a metric whose entries are constant
- Or in GR terms, the vanishing of the Riemann curvature tensor

Metric of a 2-Sphere

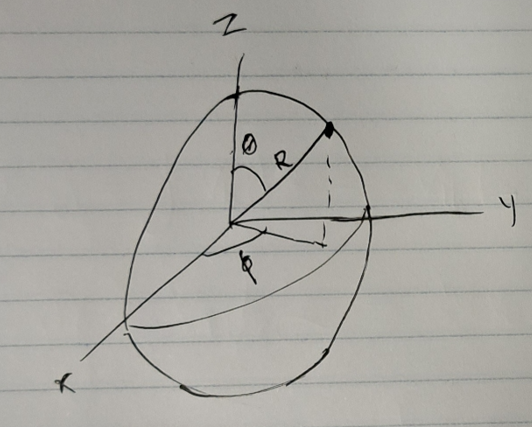
2SphereDiagram

Embbed a sphere of radius $R$ in $\mathbb{R^{3}}$
- $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}= R^{2}$ (definition of sphere/ constraint equation)
- $dl^{2} = dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}$ (definition of distance in $\R^{3}$)
- replace $dx_{3}^{2}$ by taking the total derivative of the constraint equation and eliminating $x_{3}$. You eventually get
  - $dl^{2}=dx_{1}^{2}+dx_{1}^{2}+\frac{x_{1}dx_{1}+x_{2}dx_{2}}{R^{2}-x^{2}{1}-x^{2}{2}}$
- Convert to polar coordinates ($x_{1} = R\sin(\theta)\cos(\phi)$ and $x_{2} = R\sin(\theta)\sin(\phi)$) and simplifying:
  - $dl^{2}=R^{2}(d\theta^{2}+\sin^{2}(\theta) d\phi^{2})$
  - This is the metric of the 2 sphere
Is the 2-sphere Euclidean?
- In Euclidean space, the ratio of the circumference to the radius is $2\pi$
What is the radius of a circle on a 2-sphere?
- Align the z-axis with the center of the circle. The circle is then at a fixed $\theta$ where $\phi$ varies from $0$ to $2\pi$
- Therefore, the circumference equals $\int_{0}^{2\pi} R\sin(\theta)d\phi = 2\pi R \sin(\theta)$
- The radius is $a=\int_{0}^{\theta}Rd\theta=R\theta$
- hence the ratio of the circumference to the radius is less than $2\pi$

Metric of the 3-sphere

Embed a 3-sphere in $\R^{4}$
- $r^{2}+x_{4}^{2}= R^{2}$ (definition of sphere/ constraint equation)
  - $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}= r^{2}$
- $dl^{2} = dx_{1}^{2}+dx_{2}^{2}+dx_{3}^{2}+dx_{4}^{2}$ (definition of distance in $\R^{3}$)
- Do the same process as the 2-sphere to eliminate $dx_{4}$ from the distance measure (differentiate constraint, eliminate $x_{4}$ in constraint, plug into metric, write in spherical coordinates)
  - $x_{1} = r\sin\theta\cos\phi$
  - $x_{2} = r\sin(\theta)\cos\phi$
  - $x_{3} = r\cos(\theta)$
- You eventually get the following metric:
  - $dl^{2}=\frac{R^{2}dr^{2}}{R^{2}-r^{2}}+r^{2}d\theta^{2}+r^{2}\sin\theta d\phi^{2}$
  - Alternatively: $dl^{2}=\frac{dr^{2}}{1-\frac{r^{2}}{R^{2}}}+r^{2}d\Omega^{2}$

Metric of the Pseudosphere (hyperbolic geometry)

The constraint becomes:
- $x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2} = -R^{2}$
- $dl^{2}=\frac{R^{2}dr^{2}}{R^{2}+r^{2}}+r^{2}d\theta^{2}+r^{2}\sin\theta d\phi^{2}$
- As $R\rightarrow\infty$ you recover flat space
You can also make the following subtitutions:
- $K=1\rightarrow r=R\sin\chi$
- $K=-1\rightarrow r=R\sinh\chi$
- $K=0\rightarrow r=\chi R$
These transformations convert the metric to:
- $dl^{2}=R^{2}[d\chi^{2}+\sigma^{2}(\chi)d\Omega^{2}]$
  - $\sigma(\chi) = \sin\chi$
  - $\sigma(\chi) = \sinh\chi$
  - $\sigma(\chi) = \chi$
- You can interpret $\chi$ as a distance parameter (ie. a surogate to r)
Alternatively:
- $dl^{2} = \frac{dr^{2}}{1-Kr^{2}}+r^{2}(d\theta^{2}+\sin^{2}(\theta)d\phi^{2})$
  - $K = \frac{1}{R^{2}}$,$\frac{-1}{R^{2}}$,$0$ for spherical, hyperbolic and flat geometries respectively
To calculate radii and circumference on the 3-sphere, set $\theta = \frac{pi}{2}$ for simplicity. This also implies that $d\theta=0$
- Circumfrence $C = \int_{\theta=\frac{\pi}{2}} dl = 2\pi R \sin(\chi)$ where theta and radius $\sin(\chi)$ are fixed
- Radius $R = \int_{0}^{\chi}Rd\chi=R\chi$
- Note that $\frac{C}{R}$ is not $2\pi$
What is the volume element?
- Take the negative square root of the of the determinant of $g_{\mu\nu}$ (for the 3-sphere, $g_{ij}$ is a diagonal matrix. Don’t forget to include the time component to use this rule!)
  - Ex. for the 3-sphere $V = \int_{0}^{\pi} d\chi \int_{0}^{\pi} d\theta \int_{0}^{2\pi} d\phi R^{3}\sin^{2}(\chi)\sin(\theta) = 2\pi R^{3}$
For the surface element, you ignore the radial term (ie. drop the term associated with $d\chi$)

Most general homogeneous isotropic metric

$ds^{2} = c^{2}dt^{2}-R^{2}a^{2}[d\chi^{2}+\sigma^{2}(\chi) d\Theta^{2}]$
$a(t_{0}) = 1$ is the scale factor at the present time
Say we want to find the distance between two comoving observers.
- We need to measure the distance at a fixed time ($dt=0$). We also fix $\theta$ and $\phi$ to get
  - $ds = Ra(t)d\chi \rightarrow \frac{ds}{dt} = R d\chi \dot{a} \rightarrow V = \frac{\dot{a}}{a}(aRd\chi) = Hd$
  - Because Hubble’s law falls out of this metric (the R-W metric), this shows that this metric is homogeneous

What is $a(t)?$

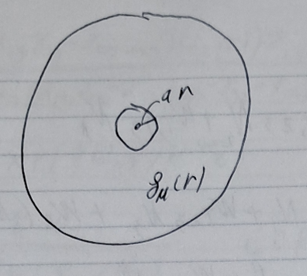
Birkhoff’s Theorem

Imagine a disk with a hole in the center. The hole has radius $a(t)R$
There exists $\rho_{\mu}(r)$ in this volume (which represents a volume element of the universe)
Make the hole small enough so that you can remove the mass inside the hole
- Assume Birkhoff’s Theorem: An empty cavity surrounded by a spherically symmetric mass distribution has the Minkowski spacetime geometry (a fancy way of saying that since there is no gravitational field inside the cavity, you can use SR inside the hole)
Place a small mass $m$ on the boundary between the hole and the volume, and Place mass $M$ at the center of the hole
The density inside the hole is $\rho_{in} = \frac{M}{\frac{4\pi}{3}(aR)^{3}}$
Using conservation of energy:
- $\frac{m(R\dot{a})^{2}}{2}-\frac{GMm}{aR}=K$
  - Multiply by $\frac{a^{2}}{R^{2}}$ and redefine the mess on the RHS as K to get
  - $(\frac{\dot{a}}{a})^{2} -\frac{8\pi G\rho}{3} = \frac{-Kc^{2}}{a^{2}R^{2}}$ (Friedmann 1)
    - interpret K as the Gaussian curvature ($K=0,\pm1 $). Also interpret $\rho$ as the mass energy density
      - $\rho = \rho_{m}+\rho_{r}+\rho_{\Lambda}$, where $\rho_{m}$ is the mass density,$\rho_{m}$ is the radiation density,$\rho_{\Lambda}$ is the dark energy density
  - Define $\rho_{c} = \frac{3H^{2}}{8\pi G}$ as the critical density
  - Define $\Omega = \frac{\rho}{\rho_{c}}$
  - You can rewrite the time-evolution of $a(t)$ as :
    - $1-\Omega = \frac{-K}{a^{2}R^{2}H^{2}}$
What all this means is that since you can measure $\Omega$ today (this sets $a(t_{0})=1$), you can tell what the geometry of the universe is (by measuring the sign of K)
- This also motivates why $p_{c}$ is called the critical density. It tells you the boundary between different large-scale geometries

Adiabatic expansion

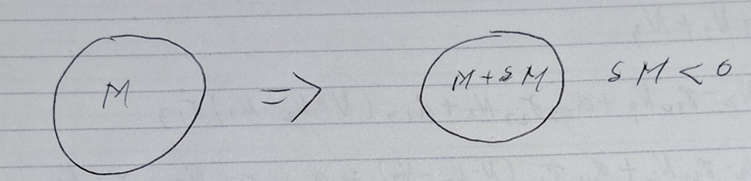
AdiabaticExpansionUni

Assume adiabatic expansion $dE+PdV = dQ = 0$
Assume that you start with a universe of total mass M. * As the universe expands, the universe loses some mass (ie. uses some energy) in order to expand (ie. $\dot{M}<0$)
$\frac{m\dot{a}^{2}}{2}-\frac{GMm}{a}= K{'}$
Take the derivative w.r.t. time (don’t forget that mass changes over time)
$\frac{dE}{dt} = \dot{E} = \dot{M}c^{2} = -P\frac{dV}{dt} = -P\dot{V}$ from the the adiabatic assumption
We know (setting R=1) that $\dot{V} = 4\pi a^{2}\dot{a}\rightarrow \dot{M} = 4\pi a^{2}\dot{a}P$
After some algebra, we get $\frac{\ddot{a}}{a} = \frac{-4\pi G}{c}(\rho+3P)$ (Friedmann 2)
- We view the $3P$ term as an effective mass term
$\frac{d(\rho V)}{dt} = P\frac{-dV}{dt}$
- Take time derivatives and substitute in volume (and derivative of volume) of the 2-sphere (use 2-sphere instead of 3-sphere because dealing with local patch of spacetime) to reach
- $\dot{p} = -(\rho+P)3H$

Friedmann Equations Summary

F1: $(\frac{\dot{a}}{a})^{2} = \frac{8\pi G}{3}\rho(a) - \frac{K}{a^{2}R^{2}} =\rightarrow H^{2}(1-\Omega_{t}) = \frac{-K}{a^{2}R^{2}}$
- $\Omega_{T} = \frac{\rho_{m}+\rho_{r}+\rho_{\Lambda}}{\rho_{c}}$
F2: $\frac{\ddot{a}}{d} = \frac{-4\pi G}{3}(\rho+3P)$
F3: $\dot{\rho} = -3H(\rho+P)$

Pure Matter Energy Density

The order of magnitude of the CMB is about 1E-4 eV. The mass of a proton is about 1E9 eV. This means we can, for simplicity, ignore the pressure term for now
Using F3, make the zero pressure assumption, substitute in the definition of $H = \frac{\dot{a}}{a}$, turn the differential equation crank yields that
- $\rho_{m}$ ~ $a^{-3}$
- Alternatively, $\rho_{m} = (1+Z)^{3}\rho_{m0}$

Pure Radiation Energy Density

From Thermodynamics, we know that for photons : $P_{r} = \frac{1}{3}\rho_{r}$
Plug into F3, turn the crank yields $\rho_{r}$ ~ $a^{-4}$
- As you expand a volume element of photons, the number of photons is fixed, but the volume drops by $a^{-3}$. The extra a term comes from redshifting

Dark Energy

$\dot{\rho} = \frac{-3\dot{a}}{a}(\rho_{\Lambda}+P_{\Lambda})$
- A very standard model of dark energy posits that $P_{\Lambda} = -\rho_{\Lambda} \rightarrow \rho_{\Lambda} = constant\rightarrow \dot{\rho_{\Lambda}} = 0$

q

Define $q_{o} = \frac{-\ddot{a}a}{\dot{a}^{2}}$
Using F2 (we can ignore radiation density and make the pressureless assumption on mass pressure)
- $\frac{\ddot{a}}{a} = \frac{-4\pi G}{3}(\rho_{m}-2\rho_{\Lambda})$
  - This means that the matter causes the universe expansion to slow down over time, while the dark energy accelerates the expansion

Age of the Universe

$H_{0}^{2} = \frac{8\pi G}{3} \rho_{co}(\frac{\rho_{m}}{\rho_{co}}+\frac{\rho_{r}}{\rho_{co}}+\frac{\rho_{\Lambda}}{\rho_{co}}+\frac{\rho_{k}}{\rho_{co}})$
- We cheat a little and pretend that the curvature is actually an energy density
- We can substitute all the $\rho$ with the approriate redshift formula to yield
$H^{2}(z) = H_{0}^{2}[\Omega_{mo}(1+Z)^{3}+\Omega_{ro}(1+Z)^{4}+\Omega_{ko}(1+Z)^{2}+\Omega_{\Lambda}]$
- $\Omega_{m0}+\Omega_{r0}+\Omega_{k0}+\Omega_{\Lambda} = 1$
$a(Z) = \frac{a_{0}}{(1+Z)}$
$\dot{a}(Z) = \frac{a_{0}\dot{Z}}{(1+Z)^{2}}$
Plugging into the definition of H and mixing terms yields
- $\frac{dt}{dz} = \frac{-1}{H(Z)(1+Z)}$
  - Replacing $H(z)$ in terms of $H_{0}$ and the energy densities, and integrating from $z = \infty$ (infinite redshift) to $z=0$ (current location)
  - $T_{u} = \int^{0}{\infty}dt = \int{\infty}^{0} \frac{dz}{H_{0}[\Omega_{m0}(1+Z)^{3}+\Omega_{r0}(1+Z)^{4}+\Omega_{\Lambda}+\Omega_{k0}(1+Z)^{2}]}$
    - $\Omega_{mo} \approx 0.3$
    - $\Omega_{\Lambda} \approx 0.7$
    - $\Omega_{mo} \approx 4E-5$
    - $T_{u}$ becomes 13.5 Gyrs

Einstein-de Sitter Universe

Let $\Omega_{m0} = 1 = \frac{\rho_{m0}}{\rho_{c0}}$, and $\Omega_{r} = \Omega_{\Lambda} =0$
To figure out the geometry of the universe:
- $1-\Omega_{0} = \frac{-K}{a_{0}^{2}R^{2}H_{0}^{2}}$
We assume a pressureless universe, so from F1
- $(\frac{\dot{a}}{a})^{2} = \frac{8\pi G}{3} \rho_{m} = \frac{8\pi G}{3}\rho_{co}(\frac{\dot{a}}{a})^{3} = H_{0}^{2}(\frac{\dot{a}}{a})^{3}$ where the second equality comes from F3
- Taking the square root and integrating a from 0 to $a(t)$ and time from 0 to t to yields
  - $\frac{2}{3}a(t)^{\frac{3}{2}} = H_{0}a_{o}^{\frac{3}{2}}t \rightarrow a(t) = (\frac{3}{2}H_{0}t)^{\frac{2}{3}}a_{0}$
  - This means that the age of the universe in this model is $T_{u} = \frac{2}{3}H_{0}^{-1}$ (set $a_{0}=1$ and set the time to be the current age of the universe $T_{u}$)
- Problem: $T_{u}$ is about 9 GYr since $H_{0}$ is 14. There are some objects that are older than this

Einstein Static Universe

We slap on the curvature energy density and a fudge factor $\Lambda$ (the cosmological constant) to F1
- $(\frac{\dot{a}}{a})^{2} = \frac{8\pi G\rho_{m}}{3}-\frac{K}{a^{2}R^{2}}+\frac{\Lambda}{3}$
- Specify that $\dot{a} = 0$ for a static universe
- $\Lambda = 8\pi G \rho_{\Lambda}$
Using F2: $\frac{\ddot{a}}{d} = \frac{-4\pi G}{3}(\rho_{m}+3P_{m}+\rho_{\Lambda}+3P_{\Lambda})$
- $P_{m}=0$ and $P_{\Lambda} = -\rho_{\Lambda}$
Setting $\dot{a}$ and $\ddot{a}$ to zero and crunching the algebra yields that $\frac{4\pi G}{3}\rho_{m} = \frac{Kc^{2}}{a^{2}R^{2}}$. This means that $K =1$ and $\Lambda = \frac{3C^{2}}{a^{2}R^{2}}$
The problem with this model is is not stable to as time evolves

deSitter Universe

Let $\rho_{r} = \rho_{m} = 0$ and $\rho_{\Lambda} = -P_{\Lambda}$
Using F2: $\frac{\ddot{a}}{a} = \frac{-4\pi G}{3}(\rho_{\Lambda}+3P_{\Lambda})$
Hence $\ddot{a} = \frac{8\pi G}{3}a \rho_{\Lambda} \rightarrow a(t) = a(0)exp(t\sqrt{\frac{8\pi G}{c}\rho_{\Lambda}})$

Dark Energy versus Cosmological Constant

Let $\rho_{\Lambda} = \frac{\Lambda}{8\pi G}$ where the LHS is Dark energy and the RHS is a cosmological constant
The distinction in that in the Einstein field equations, you can either add a scalar multiple of the metric to the curvature part (the scalar is the cosmological constant), or add a vacuum energy to the energy part (dark energy)

Inconsistency of Hubble’s constant

At $Z \leq 1$, you get that $H_{0} = 73.8 \pm 1.4 \frac{\frac{km}{s}}{Mpc}$
CMB data at $Z=1100$ states that $H_{0} = 67.4 \pm 0.5 \frac{\frac{km}{s}}{Mpc}$
This discrepancy corresponds to a $6\sigma$ discrepancy

Distance Measures

FRW = $ds^{2} = dt^{2}-a^{2}(t)R^{2}(d\chi^{2}+\sigma^{2}(\chi)(\sin^{2}\theta d\phi^{2}+d\theta^{2}))$

Comoving (radial) line of sight distance

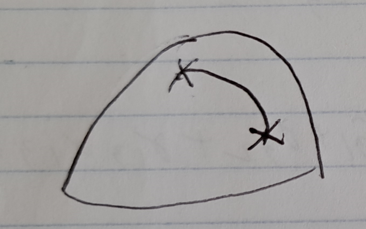
RadialDistance

Draw the shortest path between two points which being constrained onto the sphere (can be extended to other geometries)
Set $dt=0, d\phi=0, d\theta=0$ (ie a light beam geodesic), which yields that $D = \int ds = a(t_{0})R\int_{0}^{\chi}d\chi = R\chi$ (for a sphere). If you want the distance at a latter time, then $D(t) = a(t)R\chi$

Transverse Comoving distance

Also called the Angular diameter distance, or the angular diameter distance or the angular site distance or no name at all (cosmologists aren’t consistent about this)
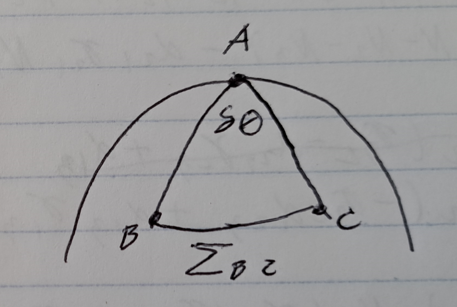
- Draw a triangle on the surface of a circle with one point on the north pole
- let the angle at the north pole be $\delta \theta$ and the corresponding arc length of $\delta \theta$ be $\Sigma_{BC}$ (called the comoving arch length)
  - $\chi_{B} = \chi_{c} = \chi$
  - $\chi_{A} = 0$
- $D_{a}\delta\theta = R\sigma(\chi)$ where $D_{a}$ is the Transverse Comoving Distance
- For a sphere, $D_{a} = R \sin\chi = d\Sigma_{BC}$

Transverse Angular Diameter Distance

Also called Angular distance or Physical Angular Diameter Distance
Draw a triangle on a sphere. Imagine that the bottom points send light at the same time towards you over a distance of $\chi$. The seperation between the bottom two is $l$.
- $ds^{2} = l^{2} = a^{2}(t_{e})\sigma^{2}(\chi)R^{2}\delta\theta^{2}$, where you use the scale factor at the time of emmission $t_{e}$

Luminosity Distance

The surface area equals $\int D_{a}^{2}d\Omega = 4\pi D_{a}^{2}$
The flux is defined as (in the frame of the galaxy) is $\frac{L_{e}}{4\pi D_{a}^{2}(1+Z)^{2}}$
The flux in our frame is $\frac{L_{0}}{4\pi D_{a}^{2}}$
- $L_{0} = \frac{dE_{0}}{dt_{0}} = \frac{dE_{0}}{dE_{e}}\frac{dE_{e}}{dt{e}}\frac{dt_{e}}{dt_{0}}$
  - First is Doppler shift, last is time dilation
$F = \frac{L_{e}}{4\pi d_{L}^{2}}$
$d_{L} = D_{a}(1+Z) = d_{a}(1+Z)^{2}$
- $d_{a}$ distance for gravitationally bound objects (measuring the size of an object spaning angle $\delta \theta$)
- $D_{a}$ used to measure seperate objects in the sky seperated by some angle
- $d_{L}$ is when you measure some flux from an object and you want the distance to the object

Horizon Distance

size of the observable universe
This is the comoving radial distance from today ($Z=0$) to the “beginning of time” ($Z=\infty$)
So if as we wait longer, the horizon distance also increases

Examples of Calculating Distances

$D_{a}(t) = R\chi a(t)$
- Fix $\theta$ and $\phi$
- Pass a light beam between the two observers (ie $ds = 0$)
- Hence $0 = dt^{2}-a^{2}(t)R^{2}d\chi^{2} \rightarrow \int_{0}^{\infty}d\chi = \int_{t_{e}}^{t_{0}} \frac{c dt}{R\ a(t)} = \int \frac{1+Z}{R}\frac{dt}{dz}dz$
- $D = R\chi = \frac{1}{H(Z)(1+Z)}$

Using Type-I Supernovae to Extract Cosmological Parameters

Let $\frac{L_{P}}{4\pi D_{L}^{2}} = F$ be the flux from a Type-I Supernovae where $L_{p}$ is the intrinsic luminosity and $D_{L}$ is the luminosity distance
Tabular Z and $D_{L}$ and plot
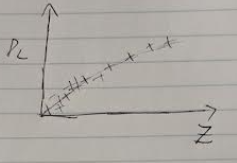
Let $D_{L} = D_{L}(Z,\Omega_{m0},\Omega_{r0}, \Omega_{\Lambda})$
We can use nonlinear fitting to extract the various parameters and figure out the age of the universe
- Can also figure out by fitting different metrics to data ($K = 0,\pm 1$). The best fit comes from $K=0$. So the universe is pretty flat.
You can also use the equation $m-M = 5\log(D_{L})$ to replace $D_{L}$ with $m-M$
- $M = -192.6\pm 0.16$

Distance Ladder

Parallax

Draw a circle that represent the earth. Draw a star(point) some distance (D) away in line with the equator. Draw a line from the antipodal points at the north and the south pole.
From basic trig, we have $D = \frac{1}{\theta}$ for small $\theta$, where D is in parsecs and $\theta$ is in arcsec.
Limited to local observations

Globular Cluster Fitting (Main Sequence Fitting)

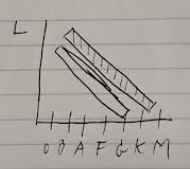
GlobularClusterFitting

Use HR diagram to identify OBAFGKM type stars based on their spectra (Tempurature increases to the left)
- Each class is subdivided into 9 subclasses
Plotting absolute magnitude/luminosity versus spectral class on the HR diagram
The linear decreasing sequence of stars define the region of main sequence stars
Looking at globular clusters, you get a main sequence that has a smaller apparent magnitude. Since you know the absolute magnitude from the original main sequence, you can calculate d with the equation
- $m-M = 5\log(\frac{d}{10\ pc})$
- You can find the d by fitting to the data

Cepheids (variable stars)

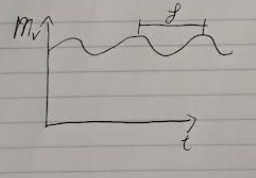
Cepheids

If you plot the visual magnitude over time, you see a periodic oscillation with period $\rho$
There exists a relationship between absolute magnitude and $\rho$. Hence, if you measure the period and the apparent magnitude, you can calculate the distance to the cepheid.
- This is good because these stars typically are quite bright
- You can see cepheids even in other galaxies

Tully-Fisher

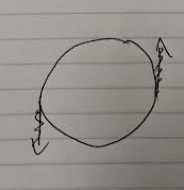
You measure spectra from gas on two diametrically opposite points of a spiral galaxy. One is blueshifted, one is redshifted
$\frac{\Delta \lambda}{2} = \lambda_{0}\beta \rightarrow \frac{v}{c} = \frac{\Delta\lambda}{2\lambda_{0}}$ since these galaxies aren’t moving relativistically
Define surface brightness as $\frac{F}{\theta^{2}} = \frac{L}{2\pi d^{2}\theta^{2}} = \frac{L}{2\pi R^{2}}$
- This implies $L = 4\pi R^{2}\Sigma$
You can use Newton’s Law to relate $v$ to $R$, and turn the crank to get
- $L = \frac{v^{4}G^{-2}}{(\frac{M}{L})^{2}\Sigma 4\pi}$
- $\frac{M}{L}$ is measured to be a constant for Type IA supernovae

Early Universe Physics

Planck Mass

The event horizon of a black hole (Schwarzschild radius) is given by $r_{s} = \frac{2GM}{c^{2}}$
The Compton Wavelength $\lambda_{c}$ is given by $\lambda_{c} = \frac{h}{Mc}$
For what mass of a black hole gives a event horizon on the order of the Compton wavelength (ie. Planck mass)?
- $M_{pl} \approx \sqrt{\frac{\pi\hbar c}{G}}$
- More rigorously, $M_{pl} = \sqrt{\frac{\hbar c}{G}}$
- The associated Planck energy and temperature is $E_{pl} = 1.2E19\ GeV = k_{b}T_{pl}$
- The Planck length is $\frac{\hbar c}{E_{pl}} = 1.6E-33\ cm$
- The Planck time is $\frac{l_{pl}}{c} = t_{pl}= 5E-44\ s$

Flatness Problem

The scale factor scales like $a(t)\approx t^{\frac{1}{2}}$ since we have a radiation dominated universe $\rho_{r=\rho}$
Since temperature scales as $a^{-1}$, this means that
- $\frac{t}{t_{pl}} = (\frac{T_{pl}}{T(t)})^{2}$
Differentiating a(t) to get that $H = \frac{\dot{a}}{a} = \frac{1}{2t}$
$\frac{|\Omega_{0}|}{\Omega_{0}} = \mathscr{E} \leq 0.01$ today (ie $\Omega_{0} \approx 1$)
What was $\mathscr{E}$ at earlier times?
- $\mathscr{E} = \frac{c^{2}}{H_{0}^{2}a_{0}^{2}R^{2}}\frac{1}{\Omega_{0}}$. There is an analagous version for $\mathscr{E}$ at any time. Take the ratio of these and simplify
- $\frac{H_{0}^{2}\Omega_{0}}{H^{2}a^{2}\Omega} = \frac{(1+Z)^{2}}{E^{2}(z)}\frac{\Omega_{0}}{\Omega}$
- $\frac{\Omega_{0}}{\Omega} = \frac{\frac{\rho_{0}}{\rho_{c0}}}{\frac{\rho}{\rho_{c}}} = \frac{H^{2}}{H_{0}^{2}(1+Z)^{n}}$
- Turn the crank to get $\frac{|\Omega_{0}|}{\Omega} = \frac{\mathscr{E}}{(1+Z)^{n-2}}$
Let n=4 (radiation dominated)
- $1+Z = \sqrt{\frac{t_{0}}{t}}$
- $\frac{|\Omega_{0}|}{\Omega} = E(\frac{t}{t_{0}})$
Epochs of the Universe
- Now: 2E10 years with $\mathscr{E}=\mathscr{E}_0$
- Nucleosynthesis: 1 sec with $\mathscr{E}=1E-18\mathscr{E}_0$
- EW scale: 1E-10 sec with $\mathscr{E}=1E-28\mathscr{E}_0$
- GUT: 1E-35 sec with $\mathscr{E}=1E-53\mathscr{E}_0$
- Planck: 1E-43 sec with $\mathscr{E}=1E-61\mathscr{E}_0$
Why was the universe almost, but not exactly, flat near the beginning of time?
- $|1-\Omega(t)| = \frac{-c^{2}}{a^{2}h^{2}l_{pl}^{2}}$
- $a(t_{pl}) = 1$,$a(t_{i}) = a(t_{pl})\sqrt{\frac{t_{i}}{t_{pl}}} = \frac{T_{pl}}{T_{GUT}}$ where $t_{i}$ corresponds to the beginning of inflation, $T_{GUT} = 1E16\ GeV$, $T_{pl} = 1E19\ GeV$
  - Dark matter energy density dominates after $t_{i}$, creating an exponentially expanding universe (deSitter) ($a(t) = a(t_i)exp(H(t-t_{i}))$)
  - $|1-\Omega_f|=\frac{-c^{2}}{H_{f}^{2}l_{pl}^{2}a(t_i)^2}$
  - Let $H_{f} = \frac{1}{t_{i}}$ because the time of inflation is the only relevant time scale of the problem
  - $(\frac{t_i}{t_{pl}})^{2}\frac{e^{-2x}}{a^2} = 1E-53\mathscr{E}$ where $x = \frac{t_f-t_i}{t_i}$
  - Turning the crank yields $x=71$
    - $t_i$ is 5E-38 sec and $t_f$ is 4E-36 sec
  - Inflation causes the universe to suddenly become flat due to the very quick introduction of dark matter

The Horizon Problem

CMB: radiation leftover from the Big Bang. $T\approx 2.73 K$
$\frac{\Delta T}{T} = 1E-5$. Ie. Isotropically, the mean deviation from 2.73 K is 1 part in 100 thousand
- This means that all points in the sky were in causal contact in the past
- Let the metric be the flat FRW metric $ds^{2} = dt^2-a^2(t)R^2[d\chi^2-\chi^2 d\Omega^2]$
- Make the coordinate transformation $d\eta = \frac{dt}{a(t)}$ and $r = R\chi$ to get that $ds^{2} = a^{2}(\eta)[d\eta^2-dr^2]$
  - The light cones of $\alpha$ and $\beta$ at the surface of last scattering cannot meet each other due to the short time between recombination time and the beginning of the universe
  - This contradicts the uniform temperature of the CMB

Solving the Horizon Problem

Let’s examine the future light cone from the recombination time to the current time
- $R\chi_a = \int_{t_d}^{t_0}\frac{c dt}{a(t)}$ where $a(t) = (\frac{t}{t_0})^\frac{2}{3}$ for a matter dominated universe
- Integration yields $3ct_0(1-(\frac{t_0}{t})^\frac{1}{3})\approx 3ct_0 = R\chi_a = D_a$
We can perform a similar calculation from the beginning of time to the recombination time
$D_{acoustic} = R\chi_{acoustic} = \int_0^{t_d} \frac{c}{\sqrt{3}}\frac{dt}{a(t)}$ where we use $\frac{c}{\sqrt{3}}$ due to the reduce propagation of light in the early universe (from $\sqrt{\frac{dP}{d\rho}}= c_{s}$)
- $a(t) = a(t_d)(\frac{t}{t_d})^\frac{1}{2}=\frac{1}{1+Z_d}\sqrt{\frac{t}{t_d}}$ for a radiation dominated universe
- This implies that $D_{acoustic} = \frac{2c}{\sqrt{3}}t_{d}(1+Z_d)$
Calculating the Transverse Angular Distance $\delta\theta_n = \frac{R\chi_n}{D_a} = 2 \frac{2t_{d}(1+Z_d)}{3t_0}$ where the extra 2 comes from taking into account both directions of propagation
Plugging in numbers ($t_{d} = 1E5\ Yr$, $Z_{d}=1300$, $t_{0}=1E10\ Yr$) to get $\delta\theta_n = 1.2\degree$
The exact calculation interpolates between radiation and matter dominated
The physical distance during inflation is then $\chi_n(t) = \frac{(\frac{\dot{a}}{a})^{-1}}{a(t)} = H^{-1} e^{-H(t-t_{i})}$
We can compare the physical distance to the horizon distance and calculate what $x = \frac{t_{f}-t_{i}}{t_i}$ is $\frac{2c}{\sqrt{3}}t_{pl}\sqrt{\frac{t_i}{t_{pl}}}e^{H(t_f-t_i)}\sqrt{\frac{t_d}{t_f}} \geq 4ct_d$ where $H = \frac{1}{t_i}$

Decoupling Time/Radiation Recombination Time

This is the time after which the universe became transparent and allowed long distance propagation of radiation
In the beginning, there was a soup of ionized Hydrogen, eletrons and photons (and some other things, not important right now)
After a certain point, the universe is cool enough that Hydrogen no longer gets ionized. This means that the reaction $H+\gamma \rightarrow H^{+}+e^{-}$ no longer dominants.
Recombination causes the hydrogen ions recombine with the electrons, allowing the photons to propagate
Naively, you would expect that once the universe cools to 13.6 eV, this recombination would happen
- In reality, you need to cool to about 0.4 eV since the Stefan Boltzmann distribution has a long tail that allows hydrogen to remain ionized longer

Dark Matter Evidence

Rotation curves

Rotation curves consist of gas clouds in galaxies
- Plots speed of galaxy versus distance to galaxy
- Can use the 21 cm line of neutral H to measure the Doppler shift $\frac{\delta \lambda}{\lambda} = \frac{v}{c}$ (non-relativistic motion)
- We would expect that the speed increases up to a certain point as you include more mass of the galaxy, and then fall off like $r^{-1}$ by Newton’s Shell Theorem
- Instead, the rotation curve flattens out in all observed galaxies
  - This flatness extends far outside the visible distribution of stars in the galaxy
- Solution:
  - Assume a spherical distribution of matter
  - Denote $r_g$ as the extend of the visible matter and $r_h$ as the extend of a type of matter that cannot be detected via radiation
  - Assume that the amount of this new type of matter (Dark Matter) is much larger than the amount of normal matter.
  - We then have that the centripetal force on the gas cloud is given by
    - $\frac{mv^2}{r} = \frac{Gm}{r}\int_{0}^{r} \rho(r’) 4\pi r’^{2} dr'$
    - we need to figure out what $\rho(r)$ is to have a flat rotation curve (ie v independent of r)
      - Assume $\rho(r) = \frac{K}{r^{n}}$ where K and n are some constants. If we let $K = \frac{v^2}{4\pi G}$ and $n=2$, then we satisfy the above condition.
  - To calculate the mass of the dark matter, perform the integral
    - $\int_{0}^{r_h} \rho(r) 4\pi r^2 dr = \frac{v^2}{4\pi G} \int_{0}^{r_h} \frac{4\pi r^2}{r^2} dr$
    - Assuming that $v = 200 \frac{km}{s}$, $r_h = 200 kpc$, that there are about 2.5E11 stars with average mass 0.3 solar masses, we can eventually show that there is about 10 times more DM than visible matter

Dark Baryon Problem

Measurements from the CMB and theory from Big Bang neucleosynthesis yields that $\Omega_{b} = 0.0455$
Direct observation is done by adding up all the mass of the visible matter. By all metrics, only about $\frac{2}{3}$ of the baryons are accounted for. (dark baryon problem)
- Hardest baryons to find are those in the intergalactic medium, where they exists in the WHIM (warm/hot intergalactic medium). WHIM is very diffuse and thus it is difficult to detect these baryons. WHIM is also very hot (T = 1E5-1E6 K), so there should be a lot of dark baryons here that we cannot see

Gravitational Lensing

Photons are gravitationally deflected near massive objects
Assume that our source is diametrically opposite from the observer with the massive object in the center
- The apparent position is deflected from the original position by some total angle $\alpha$
- Make the semi-classical approximation that $m_{\gamma} = \frac{P}{c} = \frac{E}{c}$
- The instantaneous deflection is $\delta \alpha = \frac{dP_{\perp}}{P}$ from the small angle approximation
- $\alpha = \int \delta\alpha = \int_{-\infty}^{\infty} \frac{DP_{\perp}}{dt}\frac{dt}{P} = \int_{-\infty}^{\infty} F_{\perp} \frac{dt}{P}$
- $F_{\perp} = \frac{GM}{R^2+(ct)^2}\frac{R(Pk)}{(R^2+(ct)^2)^{\frac{1}{2}}}$
- $\alpha = \frac{GMR}{c}\int_{-\infty}^{\infty} \frac{dt}{(R^2+(ct)^2)^{\frac{3}{2}}} = \frac{2Gm}{Rc^2}$
  - Answer from GR is $\alpha = \frac{4GM}{Rc^2}$
- For objects directly behind the massive object, you get an “Einstein Ring” and continuous shapes (called strong lensing)
For weak lensing, the object is not directly behind the object, and this causes magnification and shearing of the observed galaxies

Particle Physics Theory

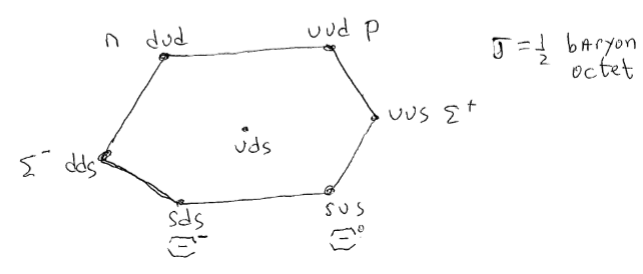
Subatomic particles

Proton and neutrons are nucleons
- consists of quarks
Leptons/quarks are point-like particles with $S = \frac{1}{2}$
- Lepton number is always conserved, while quark number is normally conserved, except in weak interactions
Particles of half integer spin are called fermions
particles of integer spin are called bosons
There are three generations/families of particles
- Each generation has two quarks, a lepton and a neutrino
  - Lightest: up and down quarks (u,d) electron $e^{-}$ and electron neutrino $\nu_{e}$
  - Medium: strange and charm (s,c) muon $\mu^{-}$ and the muon neutrino $\nu_{\mu}$
  - Heavy: top and bottom quarks (t,b) taus $\tau^{-}$ and the tau neutrino $\nu_{\tau}$
- There are corresponding antiparticles for each particle. Use $\bar x$ to denote these. Anti-leptons denoted by plus in exponent (ie. $e^{+}$)
You can denote type of quark as a flavor.
- All quarks have the same spin ($\frac{1}{2}$)
- All quarks have baryon number of $\frac{1}{3}$.
- Only the s,c,t,b quarks have their respective quantum numbers set to -1
- The charge to mass ratio $\frac{Q}{e}$ is as follows:$u = \frac{2}{3}$,$d = -\frac{1}{3}$, $s = -\frac{1}{3}$, $c = \frac{2}{3}$,$t = \frac{2}{3}$,$b = -\frac{1}{3}$
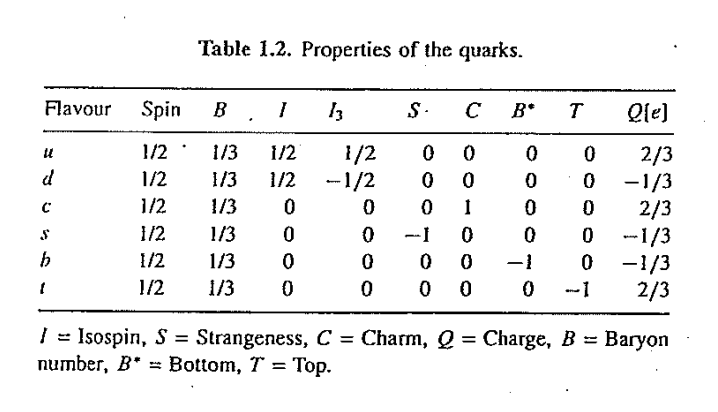
For leptons, $\frac{Q}{e} = -1$ for the electron, muon and tau and 0 for the neutrinos
- Each lepton is assigned a lepton number $L=1$
- The electron and the electron neutrino have $L_e = 1$
  - Analagous quantum numbers exists for taus and muons
The quantum numbers of antiparticles can be found by negating the quantum number of the particle
Baryons consists of particles with 3 quarks or antiquarks (qqq)
- u = uud
Baryon and lepton number is conserved in reactions
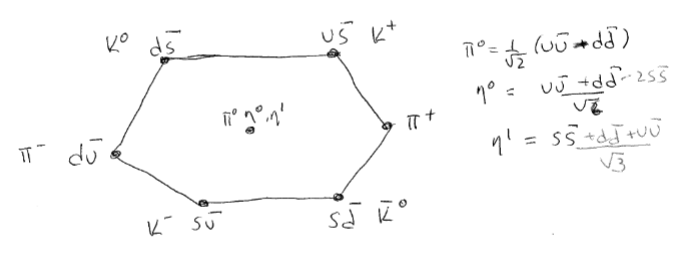
Mesons consists of particles with a $q\bar{q}$ pair
Mesons and Baryons fall under the hadrons

Force Mediators

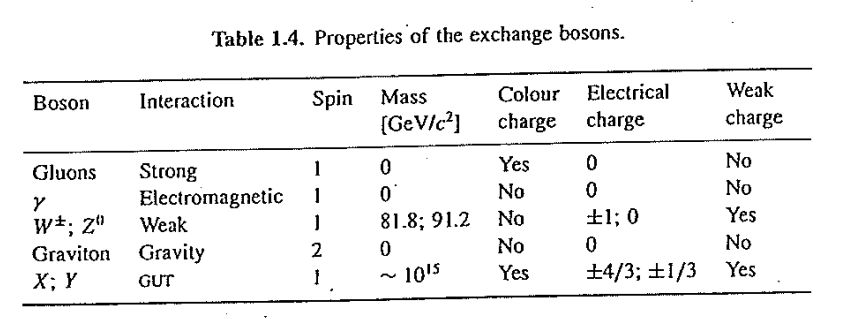
The range on each of these is governed by the Compton wavelength of the boson ($R = \frac{\hbar c}{mc^{2}}$)

Feymann Diagrams

Primary Vertices

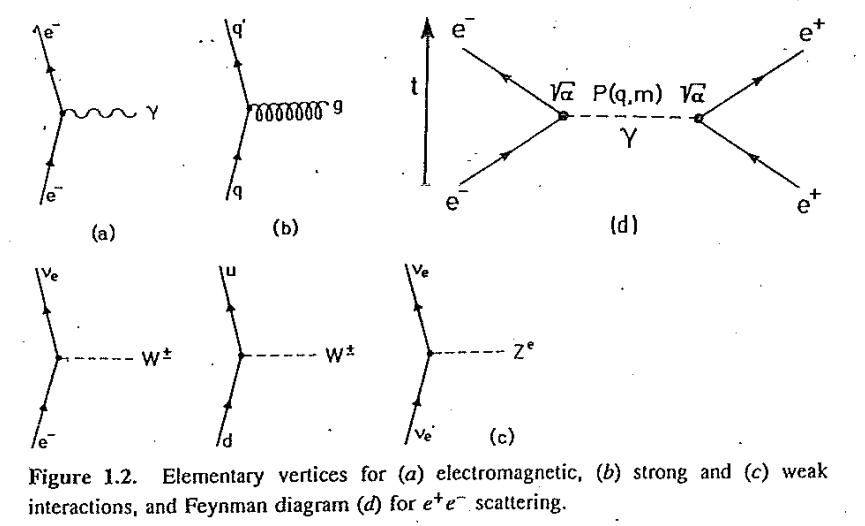
- Each primary vertex corresponds to a possible set of interactions between fermions and bosons
  - the electrons and neutrinos can be swapped out with any other lepton and it’s corresponding neutrino, as well as any anti-lepton and their corresponding antineutrino
  - same story for the quarks: q represent any of the 6 quarks or 6 anti-quarks
  - You can convert each vertex to a corresponding equation: for instance, the weak interaction involving leptons can be written out as $W^{-}\rightarrow e^{-}+\bar{v_{e}}$
    - To convert to alternative, equivalent forms, you can move particles over to the opposite side of the equation if you change it to its corresponding anti-particle and make sure that all conservation laws hold

Propagators and Probability Amplitudes

Each vertex corresponds to an amplitude proportional to the square root of some coupling constant related to its interaction ($\alpha$ for electromagnetism, $G_F$ for weak interactions etc.)
When you connect vertices to each other, this is represented by a propagator of the form $P(q,m) \propto \frac{1}{q^2-m^2}$ where m is the mass of the boson. This factor gets multiplied by the vertice amplitudes to produce the total probability amplitude
- For instance, in Fig. 1d above, the probability amplitude A is proportional to $\frac{\alpha}{q^2-m^2}$
The interaction cross section is then proportional to the square probability amplitude

Why Antimatter?

Klein-Gordan Equation

Letting $c=1$. Let the Hamiltonian be $H^2 = p^2+m^2$ and apply first quantization to the equation $H^2\psi = E^2\psi$
- $-\hbar^2 \nabla^2\psi + m^2\psi = -\hbar^2\frac{\partial^2\psi}{\partial t^2}$
- Describes a spin 0 particle

Dirac Equation

For spin $\frac{1}{2}$ particles, the Dirac equation operates on spinors, which are 4 component objects. The 1st component is a particle of mass m spin up. The 2nd component is a particle of mass m spin down.The 3rd component is an antiparticle of mass m spin up. The 4th component is an antiparticle of mass m spin down.
For Dirac, in the vacuum, there is a sea of antiparticles that occupy all the possible momentum states
- This give possible energies of $-\infty \leq E \leq -m$ for antiparticles
If you provide energy $E = 2m$, you create an electron and a hole in the Dirac sea
- The total energy of this configuration is $E = m -\Sigma_{\vec{P}\neq 0,s N_{ps} \sqrt{|P|^2+m^2}}-N_{0\uparrow}m $
  - s can be either $\uparrow$ or $\downarrow$. This means that we removed a spin up antiparticle and created a spin up particle
- We can massage the above to get that
  - $E = m -(N_{0\uparrow}M+N_{0\downarrow}M)+\Sigma_{p\neq 0,s} N_{ps}\sqrt{p^2+m^2}+N_{0\downarrow}m\rightarrow E = 2m+E_{vac}$
- We can treat the hole as a particle of mass m of opposite charge. We can’t observe this sea.
  - This is weird because there are infinities on both sides

Building Particles

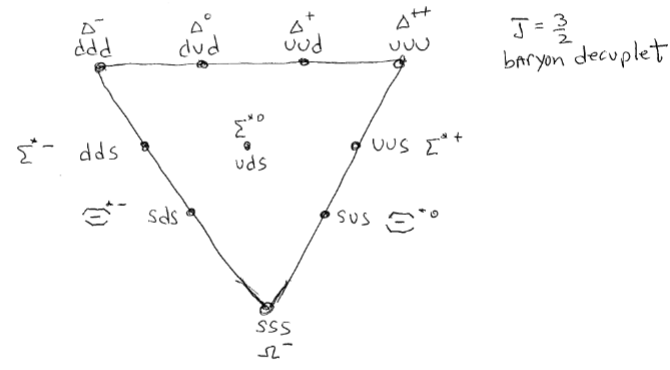
- These don’t take into account symmetry restrictions on spin and color flavor, so there are some repeats
- Note that charge Q increases from bottom left to top right, while strangeness increases as you move top to bottom

Classical and Quantum Theory of the Scalar Field

Quantitative Calculations

A reaction $a+b\rightarrow c+d$ has an associated cross section $\sigma$
- Consider shooting a beam of particles of type a at a target of type b
  - The flux of the incident particles is $\phi_a = n_a v_i$, where $n_a$ is the density of the incident beam particles and $v_i$ is the relative speed of beam compared to the target
  - The rate of particle a interactions in the target volume A dx is given as follows
    - $R= (\frac{n_b A dx \sigma}{A}) n_a v_i A$
    - The term in the parentheses tells you what fraction of incident particles interact ($n_b$ is the density of the target, A is the area of the beam, dx is the thickness of the target, and $\sigma$ is the interaction coefficient)
    - The term not in parentheses is the number of particles per second that hit the target
  - Let W be the interaction rate per target particle
    - $W = \frac{R}{n_b A dx} = \phi_a\sigma$
  - Let $dN_a$ denote the number of interactions per unit length
    - $dN_a = -(\frac{\sigma n_b A dx}{A})N_a$
    - Integrating from 0 to x yields
      - $N_a(x) = N_a0e^{-\frac{x}{\lambda}}$ where $\lambda = \frac{1}{n_b\sigma}$ is the mean free path

Fermi’s Golden Rule (2 body)

$W = \frac{2\pi}{\hbar} |T_{if}|^2 \rho_f$
- $|T_{if}|^2$ is the probability amplitude from the initial to the final states as calculated via Feynmann diagrams
- $\rho_f$ is the density of state (number of availables states in a given energy interval around final energy state)
  - $\rho_f = \frac{dN_{phase}}{dE_f}$
    - $dN_{phase} = \frac{d^3p}{(2\pi\hbar)^3}\int d^3x = \frac{Vd^3p}{(2\pi\hbar)^3} = \frac{p^2 dp d\Omega}{(2\pi\hbar)^3}\int d^3x$
      - Last step is conversion to spherical coordinates
- For these interactions, place ourself in COM such that $p_a+p_b=p_c+p_d=0$. Denote $p_f = |p_c|=p_d|$
- Define $E_f = E_c+E_d$
- $\rho_f$ is determined only by $p_f$ since all angles in phase space at a fixed $p_f$ have the same $E_f$. All of the above implies that
  - $dW = \frac{2\pi}{\hbar}|T_{if}|^2\rho_f^2\frac{dp_f}{dE_f} \frac{Vd\Omega}{(2\pi\hbar)^3}$
  - We also know that $d\sigma = \frac{dW}{\phi_i}$ where $\phi_i = n_iv_i$. We can set $n_i=1$ since eventually, the proportionality factor will cancel out the volume V in phase space.
  - $\frac{d\sigma}{d\Omega} = \frac{1}{4\pi^2 \hbar^4 v_i} |T_{if}|^2 p^{2}_{f}\frac{dp_f}{Ef}$
    - $\frac{dp_f}{dE_f} = (\frac{dE_f}{dp_f})^{-1} = \frac{d}{dp_f}(\sqrt{p^2_f+m_c^2}+\sqrt{p^2_f+m_d^2})^{-1} = (\frac{p_f}{E_c}+\frac{p_f}{E_d})^{-1}$
      - Recall that $E^2 = \gamma^2m^2 = p^2+m^2 \rightarrow 1-v^2 = \frac{m^2}{E^2} \rightarrow v^2 = \frac{E^2-m^2}{E^2} = \frac{p^2}{E^2}$
    - $\frac{dp_f}{dE_f} = \frac{1}{v_c+v_d} = \frac{1}{v_f}$ where $v_f$ is the relative speed between c and d
Hence, $\frac{d\sigma}{d\Omega}(a+b\rightarrow c+d) = \frac{1}{4\pi^2\hbar^4}|T_{if}|^2\frac{p_f^2}{v_fv_i}$
- This ignore the possible spins states. What you do is average the contributions from each combination of spin. This amounts to adding a fudging constant

Calculating $T_{if}$

Directly

Assume a Klien Gordan Potential (ie bosons). Assume a massive target (ie $p_b=0$ and $p_d=0$)
We want to find $T_{if} = \int \psi_c^* \psi_d^*g\phi \psi_a\psi_b dV$
- g is the coupling constant
- $\phi$ is interaction potential. For a Klein Gordan potential, this corresponds to $\phi = \frac{g_0e^{\frac{-r}{\lambda c}}}{2\pi r}$ since this a stationary sollution to the Kein-Gordan equation in spherical coordinates
The initial and final states take the form of plane waves: $e^{ip\cdot r}$. Since $p_b=p_d=0$, these plane waves become unity
Define $q = p_a-p_c = p_i-p_f$ as the change in momentum in the incident particle. Assume elastic collision so that no energy transfer to the target.
With all of the above, the amplitude becomes (we make a change to spherical coordinates in physical space):
- $T_{if} = \int e^{-ip_c\cdot r} g \phi e^{ip_a\cdot r} dV = gg_0 \iiint d\phi d(cos\theta) dr r^2 \frac{e^{\frac{-r}{\lambda c}}}{2\pi r} e^{iqr\cos\theta}$
- This is a straight forward, if tedious, integral. We get that $T_{if} = \frac{gg_o}{|q|^2+m^2}$
  - This is not relativistically invariant. Make the substitution of $|q|^2\rightarrow -|\vec{q}|^2$ where $\vec{q}$ represents the 4-momentum transfer between the initial and final states (ie $\vec{q} = <q_o,q>$)

Via Feynmann Diagrams

Rules

Assign a coupling strength to each vertex
Add the appropriate propagator
- For bosons, the propagator is $\frac{1}{m^2-q^2}$
square to get $|T_{if}|^2$

Cross section calculations

Early universe

Recall that $\frac{d\sigma}{d\Omega}= \frac{1}{4\pi^2\hbar^4}|T_{if}|^2\frac{p_f^2}{v_fv_i}$ where c=1
All particles are moving ultra-relativistically, hence the relative velocities $v_i$ and $v_f$ are 2. Similarly, we can say that $E = p$ since rest mass is negligible. Hence we have that $E_F = 2P_f \rightarrow E_f^2 = 4P_f^2$. In this ultra-relativistic regime, $E_f^2 = S$ is a relativistic invariant. Combining the above yields that
$\frac{d\sigma}{d\Omega} = \frac{|T_{if}|^2 S}{64\pi^2}$, which itself is relativistically invariant since $T_if$ and s are

$e^++e^-\rightarrow \mu^++\mu^-$

our force mediator is massless (ie. a photon) and our coupling constant is $\alpha = \frac{e^2}{\hbar c} \approx \frac{1}{137}$, or in natural units, $\alpha = e$
Therefore, $T_{if} = e\frac{1}{-q^2}e$
- q is change in 4 momentum from initial to final
- $q^2 = q_0^2-|\vec{q}|^2$ and $\vec{q} = p_f-p_i$
We assume elastic scatter (no energy transferred to target ie. initial and final states have same total energy ie. $q_0=0$)
Assume ultra-relativistic regime. Hence we can use early universe differential cross-section and the associated approximations, namely that $s = E_f^2 = 4p_f^2$
- We also know that $|p_f-p_i|^2 = |p_f|^2+|p_i|^2-2p_f\cdot p_i = 2p_f^2(1-\cos\theta)$ since $p_i$ and $p_f$ are the same magnitude
- $\frac{d\sigma}{d\Omega} = \frac{|T_fi|^2 S}{64\pi^2} = \frac{4p_f^2}{64\pi^2}\frac{e^4}{|q|^4}$
- $\sigma_T = \int \frac{d\sigma}{d\Omega}d\Omega = \frac{8p_f^2}{64\pi^2}\int_0^{2\pi}d\phi \int_0^{\frac{\pi}{2}}\frac{d\cos\theta e^4(\sqrt{\frac{4\pi}{\hbar c}}^4)}{2p_f^2(1-\cos\theta)}^2 = \frac{2\pi\alpha^2}{s}$
  - $\alpha = \frac{e^2}{\hbar c}$
- Exact answer $\frac{4\pi \alpha^2}{3s}$

$e^++e^-\rightarrow \gamma+\gamma$

Ultra-relativistic particles means that electron mass can be neglected
$T_if = \frac{e^2}{-|q|^2}$
Same amplitude as $e^++e^-\rightarrow \mu^++\mu^-$ since we use the same approximation; hence we have the same total cross-section

Thomson Scattering ($e+\gamma \rightarrow \gamma e$)

Has a virtual positron
$T_{if} = \frac{e^2m^2}{q_2}$
$\frac{d\sigma}{d\Omega} = \frac{s|T_{if}|^2}{64\pi^2}$
Assume $E_\gamma « m_e$ and $e^-$ at rest. Hence $q_0 = 0$ and $|q|^2$ is very small. Therefore
- $T_{if} \approx \frac{e^2}{m^2}$
$\frac{d\sigma}{d\Omega} = \frac{1}{64\pi^2}(\frac{e^2}{m^2})^2{\frac{4\pi}{\hbar c}}^2 4m^2$
- $s=E_f^2\approx 4m^2$ when $E_\gamma«m_e=m$. This gives $\sigma_T = 4\pi \frac{d\sigma}{d\Omega} \rightarrow \frac{4\pi\alpha^2}{m^2}\sigma_T$
  - Need to add $\hbar$ and c to get the correct dimensions: $\sigma_T = 4\pi(\frac{e^2}{mc^2})^2$

$\mu^++e^-\rightarrow u^++e^-$

$T_fi = \frac{e^2}{m_\gamma^2q^2} = \frac{-e^2}{q^2}$
- $Q^2 = q_0^2-|q|^2$ where $p_f-p_i$
  - Since $m_\mu = 106 MeV$ and $m_{e^-} = 0.5 MeV$ approximate this roughly elastic, so $q_0=0$ and $q^2=-|q|^2$
- In the center of mass frame, we have that $|P_i| = |P_f| = P_f$ and that $|P_f-P_i|^2 = |q|^2 = 2p_f^2(1-\cos\theta) = 4p_f^2\sin^2 \frac{\theta}{2}$
- $S = E_f^2 = (E_a+E_b)^2 = (|P_a|+|P_b|)^2 = 4p_f^2$
- $\frac{d\sigma}{d\Omega} = (\frac{e^2}{|q|^2})^2 \approx \frac{\alpha^2}{16p_f^2\sin^4\frac{\theta}{2}}$

Higher Order Corrections to $ee\rightarrow ee$

Each vertex in a Feynman diagram contributes a factor of $\alpha$
Vacuum polarization creates a pair of virtual e+e-. These virtual particles create a shielding of the nucleus
We normally get infinities for higher order corrections, but you can always isolate the infinities via renormalization (lot’s of handwaving here)
The coupling constant is not really a constant. It has a dependence on the transferred momentum
- $\alpha(q^2) = \frac{\alpha(\mu^2)}{1-\frac{1}{\pi}\alpha(\mu^2)ln(\frac{q^2}{\mu^2})}$

Weak Interactions

$W^-\rightarrow e^-+\bar{\nu_e}$
$W^+\rightarrow e^+\nu_e$
$Z\rightarrow \nu_e\bar{\nu_e}$
Neutrinos can scatter via neutral currents Z $\nu_e+\nu_e\rightarrow \nu_e+\nu_e$

e $\nu$ scattering

Can interact via either Charge current or neutral current
propagator of the form $\frac{g_w^2}{m_w^2-q^2}$
- Make the assumption that the momentum transfer is small compared to the mass of the bosons. Assuming elastic scattering:
  - $T_{if} = \frac{g_w^2}{m_w^2}$ where $q_0=0$ and $q^2\approx -|q|^2 « E_{\nu_e}^2$
Similarly, the neutral current diagram has a comparable amplitude to the charged current, therefore:
$T_{if} \approx = \frac{g_w^2}{m_w^2}+\frac{g_w^2}{m_w^2} = \frac{2g_w^2}{m_w^2}$ where $m_w\approx m_z$
$\sigma = \int \frac{d\sigma}{d\Omega}d\Omega = 4\pi \frac{d\sigma}{d\Omega} = 4\pi \frac{s|T_{if}^2|}{64\pi^2} = \frac{16\pi}{64\pi^2}\frac{g_w^4}{m_w^4}s = \frac{G_F^2S}{4\pi}$
- $G_F = lim_{q^2\rightarrow 0}\frac{g_w^2}{m_w^2-q^2}$

$e^+e^- \rightarrow \nu_e\bar{\nu_e}$

We can make the same approximation as in the electron neutrino scattering, which means that we have approximately same amplitudes. Hence $\sigma(e\nu\rightarrow e\nu) \approx \sigma(e^+e^-\rightarrow \nu_e\bar{\nu_e})$
To convert to physical units, we observe that $G_F = 1.17E-5 GeV^{-2}$
We also utilize that $\hbar c = 0.197 GeV\cdot fm$
$\sigma_{weak} \approx 1E-44 cm^2$ while $\sigma_{strong} \approx 1E-26 cm^2$. Therfore, ‘weak’ is a good moniker since the force is several order of magnitude weaker than the strong

Discovery of Color

Look at the reaction $e^+e^-\rightarrow \mu^+\mu^-$
- we know that $\sigma(e^+e^-\rightarrow \mu^+\mu^-) \propto (\frac{e^2}{q^2})S \approx \frac{e^4}{s}$
A similar relationship holds for hadrons: $\sigma(e^+e^-\rightarrow hadrons) \propto \frac{s}{q^4}\sigma_{u,d,s}(Q_i)^2 \propto \frac{e^4}{S}\sigma_{u,d,s}f_i^2$ where $f_i$ is the fractional quark charge $Q_i = f_i e$
We sum over all possible final states of the quarks
- for $E_{e^+}+E_{e^-} \le 2m_c$ where $m_c$ is the charm quark mass, the only possible final states are $u\bar{u}$,$d\bar{d}$ and $s\bar{s}$
- $f_u = \frac{2}{3}$,$f_u = \frac{-1}{3}$, and $f_s = \frac{-1}{3}$
- $R = \frac{\sigma(e^+e^-\rightarrow hadrons)}{\sigma(e^+e^-\rightarrow \mu^+\mu^-)} = \frac{3((\frac{2}{3})^2+(\frac{1}{3})^2+(\frac{1}{3})^2)}{1} = 2$
Therefore, if we observe that $R=2$ from experiment (which we do), this confirms that color exists
You also get jumps in R as you increase in energy, due to being able to produce heavier quarks (charm, bottom and top has their own jumps)

$\beta$-decay of neutron $n\rightarrow pe^-\bar{v_e}$

Recall that Golden Rule is $W = \frac{2\pi}{\hbar}T_{if}|^2\rho_f\delta(E_f-E_i)$ where the delta enforces energy conservation
$T_fi = \int\psi_p^{*}(\vec{r})e^{\frac{i\vec{p_e}\cdot\vec{r}}{\hbar}}e^{\frac{i\vec{p_\nu}\cdot\vec{r}}{\hbar}}U\psi_n(\vec{r})d^3\vec{r}$
The $\psi$ are the probabilities of disappearance and appearance of a proton and neutron respectively. The plane waves are the probability of an electron/neutrino appearing at $\vec{r}$
Let’s restrict ourselves to a box of size $L^3$. The potential is then $U = \frac{G_f}{L^2}$
We assume that the field range is smaller than $\lambda = \frac{\hbar}{mc}$. Hence, if $r >\frac{\hbar}{m_p c}$ we assume $\psi_p\approx\psi_n\approx 0$
Since $\beta$-decay produces electrons and neutrinos with energy around 10 MeV, this is much smaller than the rest mass of the proton
- $p_e « m_pc$ and $p_\nu « m_pc$
- $\frac{p_e r}{\hbar} \leq \frac{p_e}{\hbar}\frac{\hbar}{m_pc} « 1$
This above assumption remove the plane waves from the calculation: $T_{fi} \approx \frac{G_F}{L^3} \psi_p^{*}(\vec{r})\psi_n(\vec{r}) d^3r$
The proton and neutron have (roughly) the same normalized wavefunctions because they similar mass and spin.
$|T_{fi}|^2 = \frac{G_f^2}{L^6}$
$\rho_f = \frac{d^3rd^3p_e}{(2\pi\hbar)^3}\frac{d^3rd^3p_\nu}{(2\pi\hbar)^3} = \frac{L^3p_e^2dp_ed\Omega_e}{(2\pi\hbar)^3}\frac{L^3p_\nu^2dp_\nu d\Omega_\nu}{(2\pi\hbar)^3}$
- We are assuming the proton is at rest, hence no associated density of state
- $d\Omega$ is the solid angle where the particle decays into
$dp_edp_\nu = (\frac{\partial p_\nu}{\partial E_f})dP_e$ allows us to integrate out the delta function
- $dp_edp_\nu = \int (\frac{\partial p_\nu}{\partial E_f})dP_e dE_f \delta(E_f-E_i)$
$E_i = m_nc^2 = E_f = m_pc^2+\sqrt{p_e^2c^2+m_e^2c^4}+p_\nu c$
- $\frac{\partial p_\nu}{\partial E_f} = c$
Hence, $\rho(E_f) = (\frac{L}{2\pi\hbar})^6 \frac{1}{c}p_\nu^2p_e^2 dp_edp_\nu d \Omega_e d\Omega_\nu$
- $\frac{dW}{dP_ed\Omega_e d\Omega_\nu} = \frac{2\pi G_f^2 p_e^2p_\nu^2}{\hbar(2\pi \hbar)^2 c}$
Suppose that $p_\nu=0$ and the electron reaches it’s maximum energy. We can substitute this maximum electron energy for the energy of the neutrino to eliminate $p_\nu$ from the decay equation.
If the neutrino didn’t exists, then the electron would always have momentum $|p_e| = (m_n-m_p)c$. Instead, we get a distribution from $P_e=0$ to $P_e=P_{e,max}$, which is what we observe
We can integrate out the solid angles, and from energy conservation, $p_{e,max} \approx \frac{3m_ec}{2}$. Doing the integrals states that $W = \frac{G_f^2(m_ec)^5}{2\pi^3 c}$ or in physical units $W = \frac{G_f^2(m_ec^2)^5}{2\pi^3 \hbar}$
Since the lifetime of the neutron is something we can measure, we can calculate $G_f$ from this experimental value

Modern Fermi Theory

Recall that $U = \frac{e^{\frac{-r}{\lambda}}}{r}g_w^2$
The Feynmann diagram for the above is just a single vertex with no propagators (ie. no momentum transfer)
We can think of Fermi’s theory as a low energy theory, where we either have the range of the weak force go to 0, or equivalently exchange an infinite mass boson
$G_f = \frac{g_w^2}{m_w^2}$ or in physical units $G_f = \frac{g_w^2}{\hbar c}$
We see that $\frac{g^2}{\hbar c} \approx \frac{1}{120}$ while $\alpha \approx \frac{1}{137}$ for EM. Even though the couplings are about the same, the weak is much weaker than EM because of the exchange of a massive boson

Quark-Gluon Plasma

Quarks do not exists in isolation because gluons provide a quark-quark potential of the form
- $V = \frac{-4\alpha_s}{3r}+Kr$ where $\alpha_s = \frac{g_c^2}{\hbar c}$
- As r increases, the potential gets large, which keeps quarks bound
At $kr_{crit} = 2m_g$, the quarks just form a new $q\bar{q}$ pair
If you get hot enough ($T \approx 400 MeV$), then you can free quarks from this binding potential
gluons carry color charge, and hence can interact with themselves
The running coupling contant for quarks becomes $\alpha_s(q^2) = \frac{\alpha_s(\mu^2)}{1+\frac{7\pi\alpha_s(\mu^2)ln(\frac{q^2}{u^2})}{4}}$
- For $q»\mu$, we see $\alpha_s \rightarrow 0$ This is called asymptotic freedom
  - Quarks behave like free fractional point charges in extremely high energy collisions

GUTs

EM and weak couplings get stronger at higher energy and strong coupling gets weaker. There should be some energy where the couplings are around the same value (Grand Unified Theory (GUT))
Simplest GUT is SU(5), where we have the groups $SU(2)\times U(1)$ for EM/Weak and $SU(3)$ for Strong
massive force carriers imply unification
for GUTs, unification occurs via lepto-quarks bosons. Said bosons would allow a decay from quarks to leptons with an E-W coupling strength
This unification is exact in SUSY SU(5), but approximate in SU(5)

Super-K (Proton Decay)

GUTs would allow $p \rightarrow e^+ +\pi^0$ ie. proton decay. Lifetime on the order of 1E30 to 1E35 depending on your theory
Super-K searches for this by having a big tank of pure water (50,00 tonnes)
Proton’s decaying would produce relativistic decay products. In particular, the electron from this decay would produce Cherenkov light

Dark Matter Candidates

Axions a

Interacts weakly and via EM
$a\rightarrow \gamma+\gamma$
haloscope
- Imagine a microwave cavity (ie. a metal box filled with microwaves)
  - The axions have a given deBroglie wavelength, which has a particular frequency. By tuning the cavity, you can, in theory, observe this resonance frequency
helioscope
- Can use magnetic fields (B fields) to generate photons to interact with axion, and then measure the x-rays from the above reaction
  - B field has energy $\rightarrow$ can create photons from said energy which in turn can interact with the axions

Sterile neutrino $\chi$

A theoretical particle that would solve the low baseline excess at $\mu$Boone
$\chi \rightarrow \mu +\gamma$
- $m_\chi = E_\mu+E_\gamma = 2E_\gamma$ because these are ultra-relativistic particles

Light DM (ALP or axion-like particles)

They are alternate candidates to solve the dark matter candidates. That’s all they do
fuzzy DM has energy around 1E-23 eV. It is moving around at $v_g=100\frac{km}{s}$ in our galaxy. This give a wavelength of 1kpc.
$1E90 = N_a = \frac{\rho_DM}{m_a}\lambda^3$
- $\rho$ is the density of DM, m is the mass of fuzzy dark matter, and $\lambda$ is deBroglie wavelength
This forms a Bose-Einstein condensate because you have many bosons within the deBroglie wavelength
- You get a soliton (ie. black hole) at the center with radius 100 pc and the rest is a halo around this center

Stat Mech of Early Universe

Assume that we are in thermal equillibrium
$DN = \frac{d^3pd^3x}{h^3}\times f(p) \times g$
- $f(p) = \frac{1}{exp(\frac{E(p)-\mu}{kT})\pm 1}$
  - $E(p)$ is the energy of the particle and $\mu$ is the chemical potential (0 for massless particles)
  - Plus is Fermi-Dirac, Minus is Bose-Einstein
  - g is the degeneracy factor
Therefore, $ = \frac{g}{(2\pi\hbar)^3}\int d^3x \int f(p)d^3p \rightarrow n = \frac{N}{L^3} = \frac{g}{(2\pi\hbar)^3}\int 4\pi \frac{p^2}{exp(\frac{E(p)-\mu}{kT})\pm 1}dp$
$\rho = \frac{E}{V} = \frac{g}{2\pi \hbar^3}\int_{-\infty}^{\infty} E(p)f(p)d^3p$
- where $\rho$ is energy density
For WIMPs, $E(p) = mc^2+\frac{p^2}{2m}$
- This implies $n(T) = exp(\frac{\mu-mc^2}{kT})\frac{g}{(2\pi\hbar)^3}(2\pi mkT)$
- Make the approximation that $\mu_{WIMPs}=0$ since there are very few WIMPs in the universe

Ultra-relativistic particles

E=P since KE much bigger than rest mass
Let $\hbar=c=k=1$
$\rho = \frac{E}{V} = \frac{4\pi g}{(2\pi)^3}\int_{-\infty}^{\infty} \frac{E^3}{e^{E/T}\pm 1}dE$
This evaluates to $\rho_r = \frac{\pi^2}{30} g_{eff}T^4$
For bosons (minus sign), $g_{eff} = g$ and for fermions $g_{eff} = \frac{7}{8}g$
Converting back to physical units yields $\rho_R = g_{eff}\frac{\pi^2}{30}\frac{k^4T^4}{\hbar^3c^3} = \frac{1}{2}a g_{eff} T^4$
- $a = \frac{\pi^2k^4}{15(\hbar c)^3}$ ie. Stefan Boltzmann’s constant
For electrons (Fermi-Dirac), g = 2, $g_{eff} = 2\times \frac{7}{8}$ which means $\rho_r = \frac{7}{8}aT^4$
We know that $H^2 = \frac{8\pi G}{3} \rho_r$ and $G = \frac{1}{m_p^2}$ where $m_p$ is the planck mass
We know that $H = \frac{1}{2t}$
Making all the appropriate equalities yields $t = \frac{0.3}{\sqrt{g_eff}}\frac{m_p}{T^2} \rightarrow t = \frac{0.3}{\sqrt{g_{eff}}}\frac{m_pc^2}{(kT)^2}\hbar$
- This give the relationship between the time of the universe and the temperature of the universe

Family Degeneracy

2 spin states of quarks. 2 possible quarks. 3 colors
2 spins of the lepton
single state of neutrino
So for a family, $g = 3(2+2)+2+1 = 15$
$g_{eff} = \frac{7}{8}(15\times 3\times 2)$ where 15 per family, 3 families, need to include antiparticles and everything is a fermion
For the bosons, $3+3+3+1+2+8 \times 2$
- $W^{+}$,$W^{-}$ and $Z$ each are spin 1 and therefore have 3 spin states
- The Higgs $H_{0}$ is spin 0, hence only 1 state
- Photons can be right or left handed (helicity)
- The 8 gluons flavors each with helicity of 2
$T_{GUT}$ is 1E15 GeV, t = 1E-35 sec as the planck time
$\tau_{w,z} = \frac{\hbar c}{m_wc^3} \approx$ 1E-24 sec
- Lifetime of W and Z in early universe via uncertainty principle
- the W’s and Z exist for a longer period of time because of the reaction $\gamma\gamma \leftrightarrow W^+W^-$
- W lasts longer than Z because it’s lighter
A similar story happens for the hadrons
Eventually, we only have photons, protons (which don’t decay) and neutrons (which decays very slowly on the timescales we care about). The neutrons combine with the protons to create the primodial elements

Current Temperature of CMB

The neutrinos can couple to the photon field via weak interactions with leptons which in turn couple electromagnetically to the photon field
- $\nu_{i}+l_{i} \rightarrow \bar{\nu_{i}}+l_{i}$
- $l_{i}^{+}l_{i}^{-} \leftrightarrow \gamma\gamma$
Eventually, the W and Z bosons fall out of equillibrium, which causes the interaction rate to rapidly drop off as the universe cools
- Interaction rate is given by $\Gamma_{W} = \frac{\alpha^2 T_d^5}{m_{w}^4}$
- This interaction rate must be less than the expansion of the universe $H = \frac{T_d^2}{m_{pl}}$
- After reaching this $T_d$, the neutrinos cool as the universe expands (first radiation-dominated, then matter-dominated). Their current tempurature is around 1.9 K

Reheating

Eventually, the electrons will fall out of thermal equillibrium with the photon bath. At this point, all the energy of the electrons gets converted in to energy for the photons, which creates a jump discontinuity in the Temperature of the photons
- Penzias and Wilson discovered CMB via 7 cm receiver. The actual CMB peak is at 1 mm. Penzias and Wilson just had a very big antenna to catch the CMB

Neutrino Contribution to DM

In order for the 3 neutrino flavors to be the dark matter, the summed mass of the neutrinos needs to be equal to 13 eV to be consistent with cosmological measurements
The upper bound on the mass of the neutrino is about 0.1 eV. Hence, neutrinos are not a dominant dark matter component
Sterile neutrinos could still be the dark matter (ie neutrinos that only interact gravitationally and only oscillate)

WIMP Miracle

Skipping a lot of math, suppose that WIMPs were the dark matter. A WIMP of SUSY mass scale with a weak coupling would freeze out of thermal equillibrium at the right time such that you get the observed present day dark matter density

Inflationary cosmology revisited, and structure formation

The inflaton is a particle that is responsible for the expansion of the universe (inflation)
Define the action as $S \int \mathcal{L} d^4x \sqrt{|g|}$ where $\mathcal{L} = \frac{1}{2}g^{\mu\nu}\partial_{\mu}\phi \partial_{\nu}\phi-V(\phi)$
$\frac{H^2}{m^2} > 60$
$\frac{3H^2}{m^2} = \frac{8\pi G}{3}\frac{\rho_{\phi}3}{m^2} \approx \frac{8\pi G}{m^2}V(\phi)$
- We require that $\rho_{\phi} \leq \rho_{pl} = \frac{m_{pl}}{l_{pl}^2}$
  - In other words, the density of the inflaton has to be less than the density of the plank mass
  - $\rho_{\phi} \leq m^4_{pl} \rightarrow V(\phi) < m_{pl}^4$
Combining the above yields that $m < \sqrt{\frac{2\pi}{15}}m_{pl}$
- This means that we can construct a theory of the inflaton that does not require quantum gravity
$\dot{\phi}_{t} = \frac{-1}{3H}\frac{\partial V}{\partial \phi}$
- $\frac{\dot{\phi_t}}{V} = (\frac{V’}{V})^{2} \frac{m_{pl}}{24 \pi} « 1$
- Hence $(\frac{V’}{V})^{2} « 1$ (slow roll condition)
Therefore, assuming an energy minimum at $\phi_g$, we get that $\frac{1}{2} (\phi^2-\phi^2_g) m^2 = V(\phi)$
The original inflation equation of motion is
- $\ddot{\phi}+3H\dot{\phi}+\frac{\partial V}{\partial \phi} = 0$
What happens physically:
- The inflaton slow rolls
- When $\phi\rightarrow\phi_g$, all the energy becomes KE
- The friction term from the expansion of the universe $H\dot{\phi}$ dissipates the energy
- This dissipated energy creates virtual pair productions. Because of the expanding universe, these virtual pairs are pulled further than their Compton wavelength and become physical particles

Energy Scales

1E14 GeV Plank (Quantum Gravity Regime)
- Prior to the time associated with this energy, no idea
1E15 GUT scale (energy where all coupling constants unite)
- Prior is primarily radiation dominated
- During this period, inflation greatly spikes
250 GeV (Weak and EM decouple)
150 MeV (Quarks become confined)
Some time at around 1E3 years after the start of the universe, inflation slows down since DM takes over
1E-3 eV (Current CMB temperature)

Structure Formation

Imagine the inflaton oscillates
- This generates density fluctions, which in turn lead to temperature fluctions. These temperature fluctions show up on the CMB
Hence, looking at temperature fluctuations on the CMB can be a physical observable that gives info about the inflaton field
Imagine that we have 2 events A and B at the beginning of the universe undergoing slow roll. Immagine that B is higher up in the potential.
- B reaches the bottom of the potential well earlier than A (sleds on a hill). Hence, there is some $\delta t$ between the two events
  - Define $\delta = \frac{\delta p}{\rho} \approx \frac{\delta t_h}{t_h}$
    - $t_h = H^{-1}$
  - $\frac{\delta t_h}{t_h} = \frac{\delta \phi}{\dot{\phi H^{-1}}}$
- Hence $\delta = \frac{\delta \phi_h}{\dot{\phi}H^{-1}}$
- Fields also obey an uncertainty principle: $\Delta \phi_n\Delta t_n =1$
After some algebra, you get that $\delta = \frac{m^2\phi^2}{m_{pl}^2} = \frac{\Delta T}{T}$
Looking at the root mean squared average of $\delta$, you use Fourier decomposition to transform $\delta(\vec{r})$ to $\delta(\vec{k})$ in order to get the power emmitted at a given wavelength from the fluctuation in density

Transparency of the Universe

Recall the Thomson scattering cross-section ($\gamma+e\rightarrow \gamma+e$) is $\sigma = \frac{8\pi}{3}(\frac{e^2}{mc^2})^2 \approx 1E-26 cm^2$
To be opaque to light, we need that the mean free path be less than the horizon $l « 2ct_\gamma$
- l = $\frac{1}{n_e\sigma}$
- the number of electons equal the number of protons, and we can make the approximation that the number of protons equals the number of baryons
  - $n_e = n_p = n_b$
- $n_p = n_{p0}(1+Z)^3 = \Omega_{bo}\rho_{bo}\frac{(1+Z)^3}{m_p}$
  - $Z \approx 1100$ at around 100 thousand years old
  - $n_p \approx 3E8 cm^-3$. Plugging in, we get that l is less than the horizon size (1ly « 2E5 ly)
Eventually, the reaction $H+\gamma \leftrightarrow p+e^{-}$ fizzles out at some temperature

The Cosmic Microwave Background (CMB)

Observations of the CMB

First observation of CMB. Spectrum of the CMB measured Penzias Wilson
Measurement of the CMB anisotropy $\frac{\Delta T}{T}$
To be done: Polarization of primodial B-mode

Measuring CMB

A radio telescope consists of an antenna and a receiver
A telescope is defined by its solid angle, its frequency, and the discretization of its frequency ($\Delta \nu$)
- Large discretization is broadband, small discretization of frequency is narrowband
The power you receive is given by $\Delta P = I_{\nu}^{BB}\Delta\Omega\Delta\nu = \frac{h\nu^3 c^3}{exp(\frac{h\nu}{kT})-1}\Delta \nu \Delta \Omega$
- $I_{\nu}^{BB}\Delta\Omega\Delta\nu = I_{\nu}^{BB}(T)+I_{BV}$
- $I_{BV} = I_{BV}^{foreground}+I_{BV}^{detector}$
Define $T(\vec{n})$ to be the tempurature along the unit vector $\vec{n}$.
Define $<T(\vec{n})>= \bar{T} = 2.73$ as the mean and define the deviation $\frac{\delta T}{\bar{T}}$ be the fluctuation from the mean
With enough points, you can treat these functions as continuous functions. Since we are measuring on a sphere, we can approximate as follows (ie. via decomposition into spherical harmonics)
- $\frac{\delta T}{\bar{T}} = \Sigma_{l=0}^{\infty}\Sigma_{m=-l}^{l} a_{lm} Y_{lm}(\theta,\phi)$
- The observation theta dependence is $T_{obs}(\theta) = T_{cmb}(1+\frac{v}{c}\cos(\theta))$.
  - Called the dipole anisotropy

Correlation Function

Define $C(\theta) = <\frac{\Delta T(\vec{n})}{\bar{T}}\frac{\Delta T(\vec{m})}{\bar{T}}>$
- $\vec{n}\cdot\vec{m} = \cos\theta_0$ for some fixed $\theta_0$
$C(\theta) = \frac{1}{4\pi}\Sigma_{l=0}^{\infty} (2l+1) C_{l}P_{l}(\cos\theta)$
- $P_{l}(\cos\theta)$ are the Legendre polynomials for some integer l
- $c_l = <|a_{lm}|^{2}>$ is the angular power spectrum averaged over all m
The maximum power observed is given by $l = \frac{\pi}{\theta_0}$
The angular resolution is limited by $\delta \theta = \frac{1.22 \lambda}{D}$
- You cannot just build a telescope of large D because the atmosphere blocks many wavelengths

CMB Acoustic Oscillations

Light gets redshifted as it ascends into a gravitational field
- Given by (semi-classical): $\nu_{r} = \nu_{0}(1-\frac{gz}{c^2})$
- Exact value is $\nu_{r} = \nu_{0}\sqrt{1-\frac{2gz}{c^2}}$
Gauss’s Law for gravitation yields that $\nabla^{2}I = 4\pi\rho$ where $\Phi = gz$
Suppose that $\Phi(\vec{r}) = \Phi_0(\vec{r})+\delta \Phi_g(\vec{r})$
- After Fourier Transforming to wavelength, we can examine the matter contents inside one of the wells created via density fluctuations
- Soup of dark matter, electrons, protons and photons
- Two opposing processes:
  - Thompson scattering between electrons and photons creates radiation pressure that pushes the electrons out of the well
    - Radiation Pressure goes like $F = \rho \sigma \approx \frac{aT^4\sigma}{3}$
  - Columb force between protons and electrons tried to keep the electrons bound
- Lower in the well, there is a higher density of protons, photons and electrons, which increases the plasma temperature and causes the radiation pressure to get big, pushing everything out of the well
- As you climb higher in the well, density decreases and the photons get redshifted. Eventually, Columb forces overwhelm Radiation pressure and everything falls back in the well
- Process called CMB oscillations
- Described by Sachs-Wolfe Effect: $\frac{\Delta T}{T} = \frac{-(1+3\alpha)}{3+3\alpha}\Phi$
  - For large redshift (ie. Z=1100), $\alpha \approx 0$, hence we find cooler photons at the bottom of the well and hotter photons at the top of the well

Primordial Black Holes and Hawking Radiation

Looking at the GR redshift formula: $\frac{\nu_{r}}{\nu_{0}} = \sqrt{1-\frac{2gz}{c^2}}$. There exists some spherically symmetric mass distribution with radius $R_{s} = \frac{2GM}{c^2}$ such that $\frac{\nu_{r}}{\nu_{0}}\rightarrow 0$ ie. no radiation can escape from the body
Hawking radiation arises from virtual pairs are produced at the edge of the black hole
- If the virtual pairs are produced a distance of $\lambda_{C}$ from the edge of the blackhole, one of the particles can fall into the hole and fail to recombine with the other one. This creates a real particle. The energy needed to create this real particle is drawn from the gravitational field of the black hole
- The spew of these particles creates photons that flee from the black hole
- The ejection of massless particles is a general feature of a black hole
  - This implies that gravitions of mass $m=0$ are ejected, which in turn means that gravitational waves should be generated from the black hole
- As these massless particles interact with the gravitational field of the black hole, they take away energy and thus reduce the mass of the black hole

Application to Inflation

Can apply the same logic of Hawking radiation to an expanding universe
- Think of the inside of the black hole as the “exterior” of our universe and the outside of the black hole as the observable universe on the inside
- Same logic implies that you should observe gravitational waves due to inflation
  - These gravitaional waves have 2 polarizations states, which in turn cause the CMB to become polarized

Polarized CMB

At the surface of last scatter, some of the CMB photons Thompson scattered off of electrons, polarizing the photons
You can measure this polarization on the sky and break it up into E and B modes (E modes are divergence free and B modes are curl free)
- Promordial gravitational waves only produce B-mode polarizations. Hence, measuring B-modes would be indicative of their existance
  - The E-modes can get gravitationally lensed by matter and appear as B-modes
  - There is a lot of background polarized dust emission

Neutrinos

Cosmic rays produces electron and muon neutrinos via the reaction $\pi^{+} \rightarrow \mu^{+}+\nu_{\mu} \rightarrow e^{+} \mu_{e}+\bar{\nu_{\mu}}+\nu_{\mu}$
- We therefore expect the ratio of $\nu_{\mu}$ to $\nu_{e}$ to be 2. We instead get 1
- This means that some of the $\nu_{\mu}$ get turned into $\nu_{e}$ via oscillations
For the two neutrino case, we have that $P(\nu_{1}\rightarrow \nu_{2}) = 1-\sin^2(2\theta)\sin(\frac{L}{4\hbar c}\frac{\Delta m^2}{E})$ where $\Delta m^2$ is the squared mass difference between the two neutrino flavors

Super-K

Super-K can measure the neutrinos from overhead, from the horizon, and from the other size of the earth
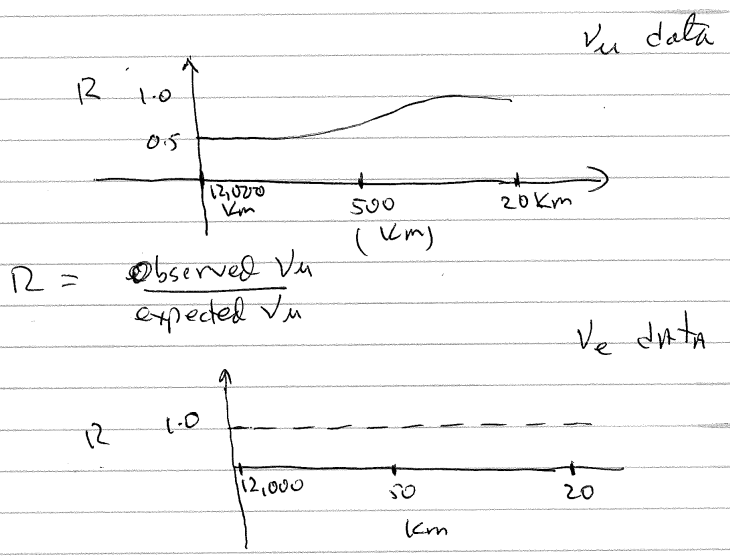
- electron neutrinos don’t seem to oscillate because the squared masses involved are smaller and electron neutrinos are produced at lower altitudes
- About half of the muon neutrinos oscillate to taus at low L since many cycles of $\sin^{2}(\frac{\Delta m^2 L}{4 \hbar c E})$ occur, which averages to 0.5

Detection Channel in Supe-K

Can detect neutrinos via charged current interaction. The $e^{-}$ produces Cherenkov rings which the PMTs can pick up and reconstruct the direction of the incident neutrino
- For muons, the ring is crisp because the muon undergoes little scattering
- For electrons, you get a fuzzy pattern
Can also have charged current interactions with the neutrinos and protons of the H20 to produce hadrons and a lepton

SNO

You put a big 1 kTon tube of heavy water underground
- You detect Cherenkov radiation produced by the scattered electrons

CC Channel

$\nu_{i}+H^2\rightarrow p+P+l_{i}$
muon neutrinos and tau neutrinos cannot use this channel since the maximum energy of neutrinos from the sun is around 15 MeV. Hence there is not enough energy to produce a muon or a tau
- Only electron neutrino can use this channel

NC Channel

$\nu_{i}+H^{2} \rightarrow p+n+\nu_{i}$
All neutrino flavors can use this channel
- This means that if neutrinos oscillate, the CC channel should measure 1/3 of the theoretical neutrino flux while the NC channel measures all the neutrino flux
- If there where only electron neutrinos (which are the only types of neutrinos produced in the sun), you would expect the CC and NC fluxes to be equal.
  - Since CC is 1/3 of NC, this means that the electron neutrinos must have oscillated to other flavors

ICECUBE

An hexagonal array of DOMS (ie. phototubes) buried deep in the ice of antartica

Detection Channels

Charged Current given by $\nu_{i}+N \rightarrow l_{i}+X$
Neutral current given by $\nu_{i}+N \rightarrow \nu_{i} +X$
In either case, this is called deep inelastic scattering
Glashow resonance $\bar{\nu_{e}}+e^{-} \rightarrow q \bar{q}$
- Only occurs at 6 PeV
electrons leave a blobby mess in the DOMS
Muons leave a long trail of energy deposits
Taus cause “double bang events”, where the first bang is when the tau is produced and the second bang is when the tau decays some distance away due to its extended life time from time dilation

Special Relativity#

Spacetime Diagrams#

Worldline#

Inertial Frames#

Postulates of SR#

Deriving Time Dilation from diagrams#

Deriving Doppler Shift from Diagram#

Metrics#

Metric tensor (SR)#

Covariant versus contravariant vectors#

Metric in Spherical Coordinates#

4-Momentum#

Example#

Classical Cosmology#

The Cosmological Principle#

Comoving Coordinates#

Hubble’s Law#

Wavelength relation to scale factor#

Luminosity Distance (L)#

Non-Euclidean Geometry#

Metric of a 2-Sphere#

Metric of the 3-sphere#

Metric of the Pseudosphere (hyperbolic geometry)#

Most general homogeneous isotropic metric#

What is $a(t)?$#

Adiabatic expansion#

Friedmann Equations Summary#

Pure Matter Energy Density#

Pure Radiation Energy Density#

Dark Energy#

q#

Age of the Universe#

Einstein-de Sitter Universe#

Einstein Static Universe#

deSitter Universe#

Dark Energy versus Cosmological Constant#

Inconsistency of Hubble’s constant#

Distance Measures#

Comoving (radial) line of sight distance#

Transverse Comoving distance#

Transverse Angular Diameter Distance#

Luminosity Distance#

Horizon Distance#

Examples of Calculating Distances#

Using Type-I Supernovae to Extract Cosmological Parameters#

Distance Ladder#

Parallax#

Globular Cluster Fitting (Main Sequence Fitting)#

Cepheids (variable stars)#

Tully-Fisher#

Early Universe Physics#

Planck Mass#

Flatness Problem#

The Horizon Problem#

Solving the Horizon Problem#

Decoupling Time/Radiation Recombination Time#

Dark Matter Evidence#

Rotation curves#

Dark Baryon Problem#

Gravitational Lensing#

Particle Physics Theory#

Subatomic particles#

Force Mediators#

Feymann Diagrams#

Primary Vertices#

Propagators and Probability Amplitudes#

Why Antimatter?#

Klein-Gordan Equation#

Dirac Equation#

Building Particles#

Classical and Quantum Theory of the Scalar Field#

Quantitative Calculations#

Fermi’s Golden Rule (2 body)#

Calculating $T_{if}$#

Directly#

Via Feynmann Diagrams#

Rules#

Cross section calculations#

Early universe#

$e^++e^-\rightarrow \mu^++\mu^-$#